問題.
\(5\)で割ると\(3\)余り,
\(3\)で割ると\(1\)余る数を
\(15\)で割ったときの余りを求めよ.
一般的には,連立合同式や一次不定方程式の問題として,
合同式やユークリッドの互除法を用いて解かれるこの問題を,
本稿では,次のように図解してみる.
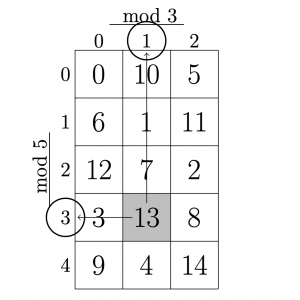
まず,右のような表を作り,
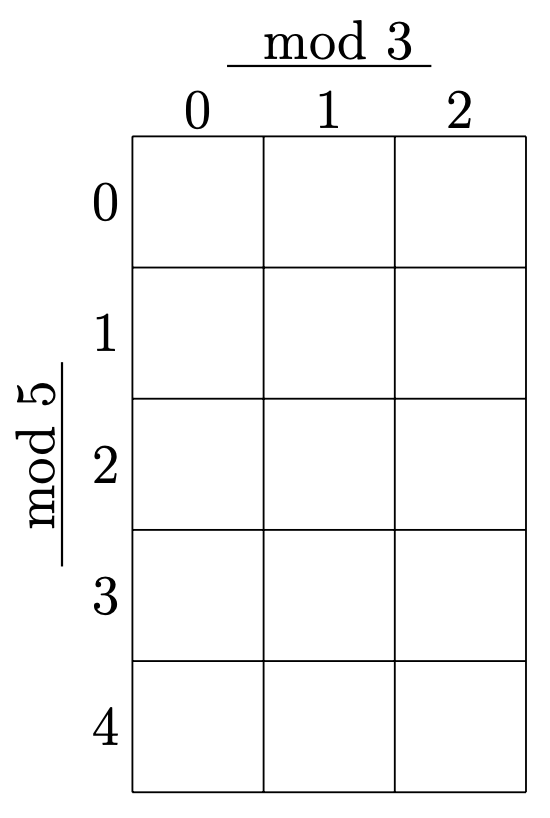
(行と列の番号は\(0\)から始まっていることに注意する)
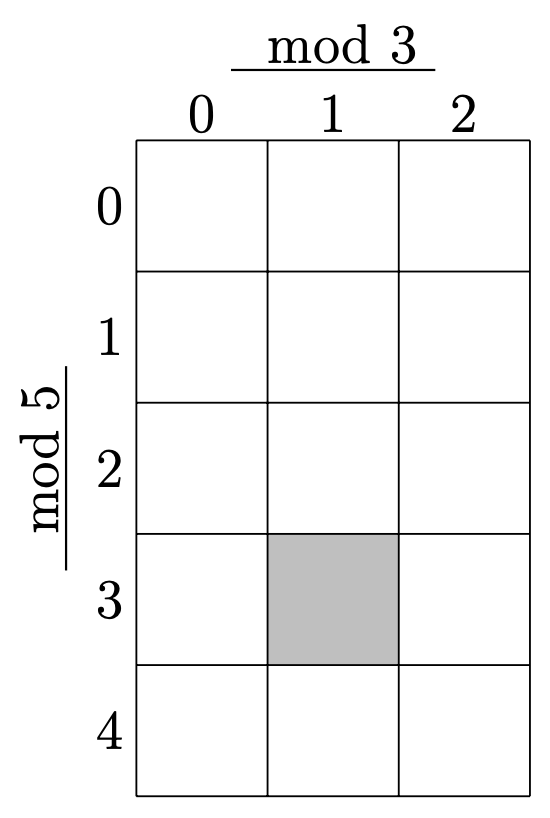
次に, 左上のマスから, 斜め右下方向に, \(0,1,2,\cdots\)と 順に数字を入れる. その際,
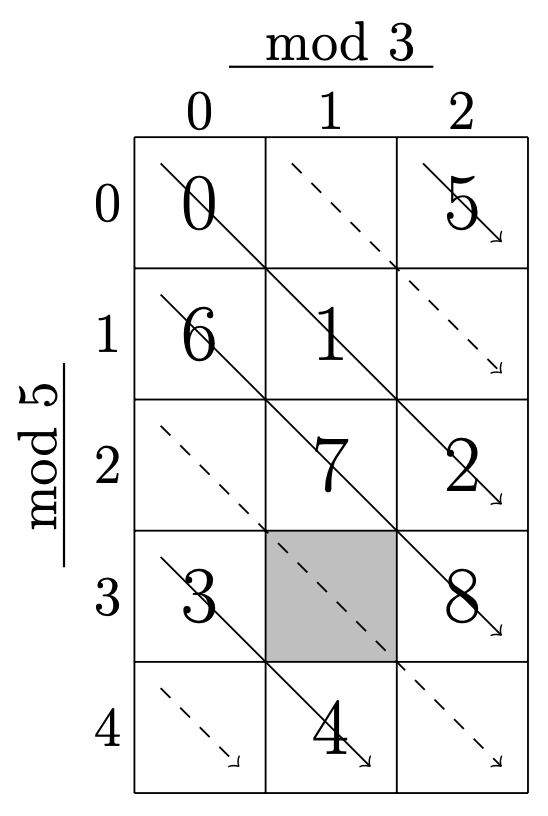
最終的に,はじめに印をつけた部分にある数字が答えである. よって,求める余りは,\(13\)である.
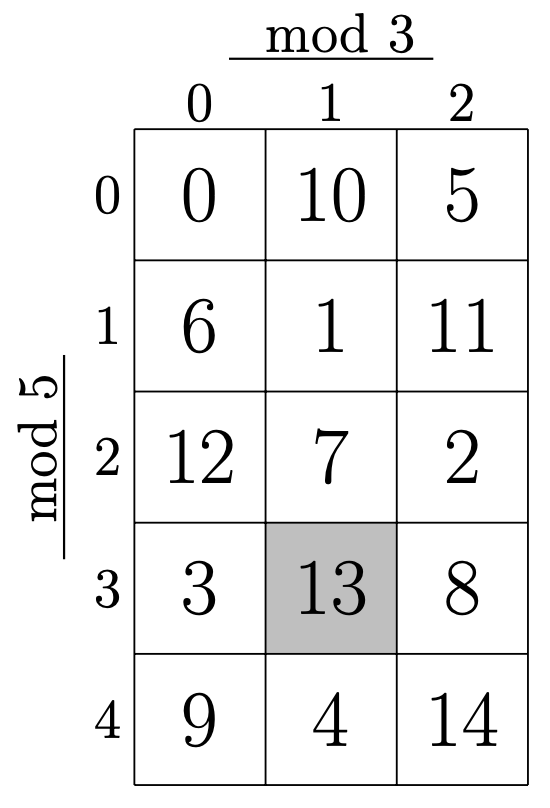
それでも,あえてこの方法を示したのは, 上の問題の背景にある中国式剰余定理の 全単射(一対一対応)が見やすいという理由からである.
定理(中国式剰余定理).
\(m_1,\ m_2\)を互いに素な自然数とし,
\(m=m_1m_2\)とする.
このとき,
$$
\left\{
\begin{array}{c}
n\equiv a_1\mod m_1\\
n\equiv a_2\mod m_2
\end{array}
\right.
$$
を満たす\(n\ (0\leq n < m)\)
が一意的に存在する.
上で述べた一対一対応を簡単に説明しよう.
自然数\(m\)に対して,集合\(R_m\)を $$ R_m:=\{0,1,2,\cdots,m-1\} $$ と定義する. このとき, 一対一対応 $$ R_3\times R_5\ni(a,b) \longleftrightarrow c\in R_{15} $$ が存在するというのが中国式剰余定理の主張である.
$$ R_{15}\ni 13 \longrightarrow (1,3) \in R_3\times R_5 $$ 側の対応(すなわち,13から組(1,3)を得ること)は簡単であるが, 難しいのは,逆側の対応 $$ R_3\times R_5\ni (1,3) \longrightarrow 13 \in R_{15} $$ である. (すなわち,組(1,3)から13を得ることである.) この難しい側の 対応を与えるということが, 上の問題を解くということなのであるが, この一対一対応をまとめたものが, 上で作った表なのである.
詳しくは,下のPDFを見ていただきたい.
