GLEAMATH BALL

青いボールをタップするまでの時間を競うだけのゲームです．良かったらどうぞ．

GAME

以下は数学的な補足です．
ボールが衝突したときのはね返り角度を計算する．
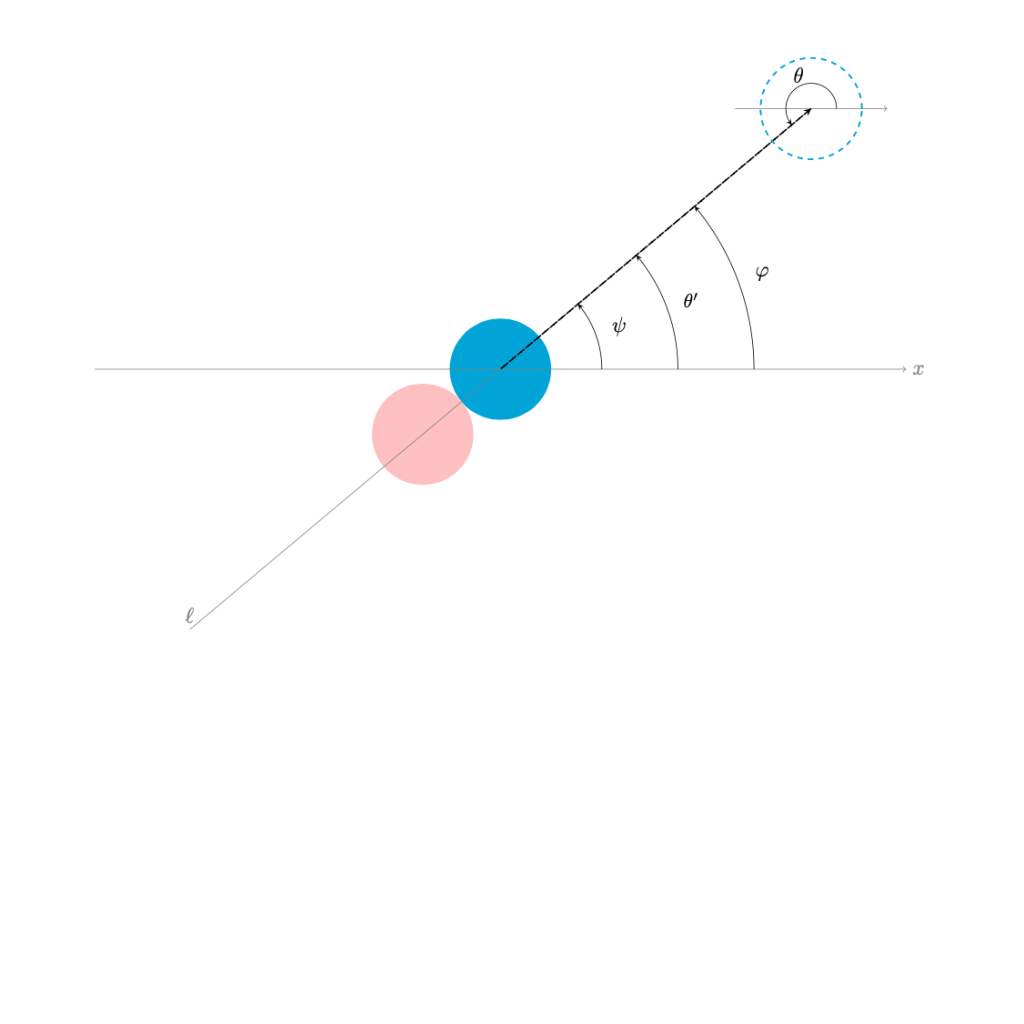
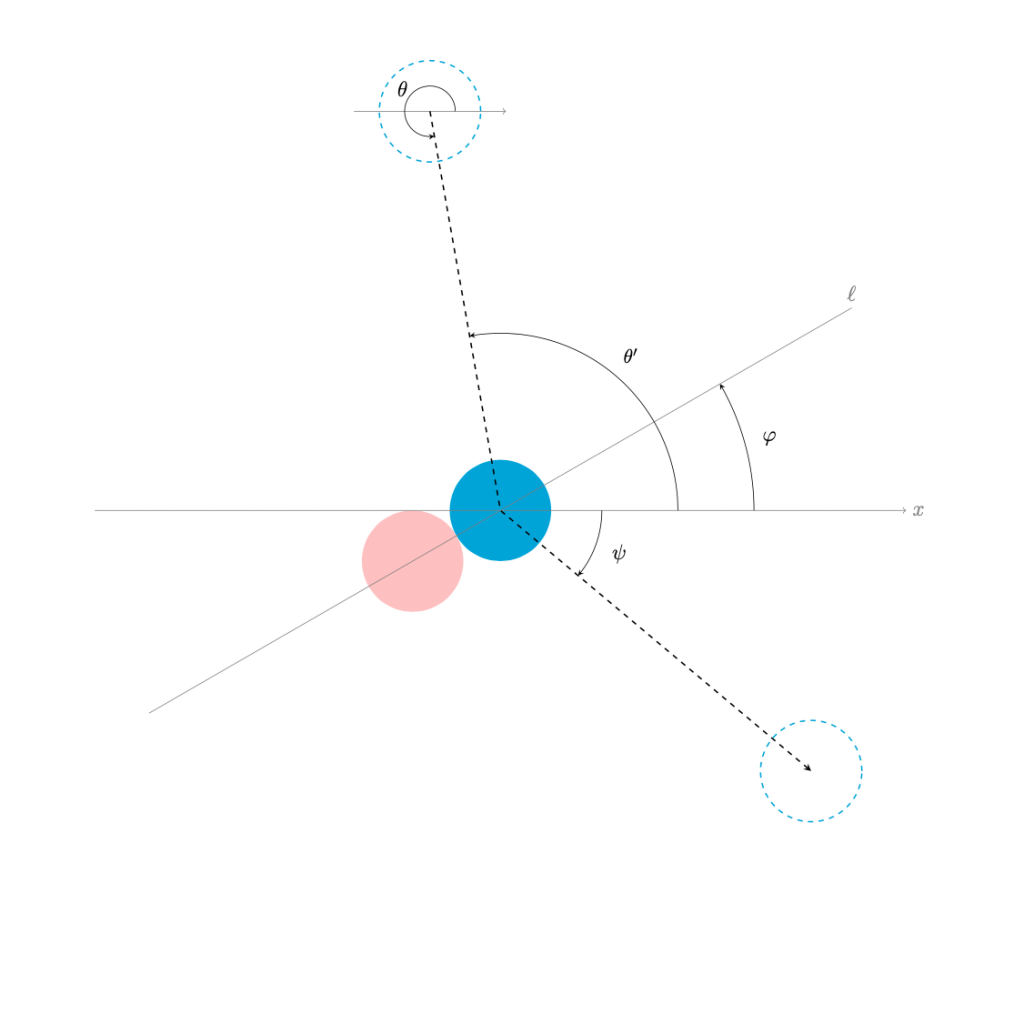
下図のように，青色のボールが止まっている赤色のボールに衝突する状況を考える．ただし，角度は全て向きも含めた（始線を$x$軸の正の部分とする）一般角で考える．

$\theta$ : 青色のボールの進む向き
$\theta’$ $:=\theta-\pi$
$\ell$ : 衝突時の赤色のボールと青色のボールの中心を通る直線
$\varphi$ : 直線$\ell$と，$x$軸のなす一般角
$\psi$ : 衝突後に青色のボールが進む向き

このとき次が成り立つ．

$$\psi \hspace{5pt}=\hspace{5pt} 2\varphi-\theta’ \hspace{5pt}=\hspace{5pt} 2\varphi-\theta+\pi$$

様々な向きからの衝突が考えられるが， $\varphi$の値を固定し， $\varphi$に対して， $\theta’=\theta-\pi$が $$\varphi-\frac{\pi}{2}<\theta'<\varphi+\frac{\pi}{2}$$ を満たす範囲で考えれば良い．
（多くのパターンをイメージできるように，以下の図ではあえて$\varphi$を一定にしていない．）

$\varphi-\frac{\pi}{2}<\theta'<\varphi$のとき，

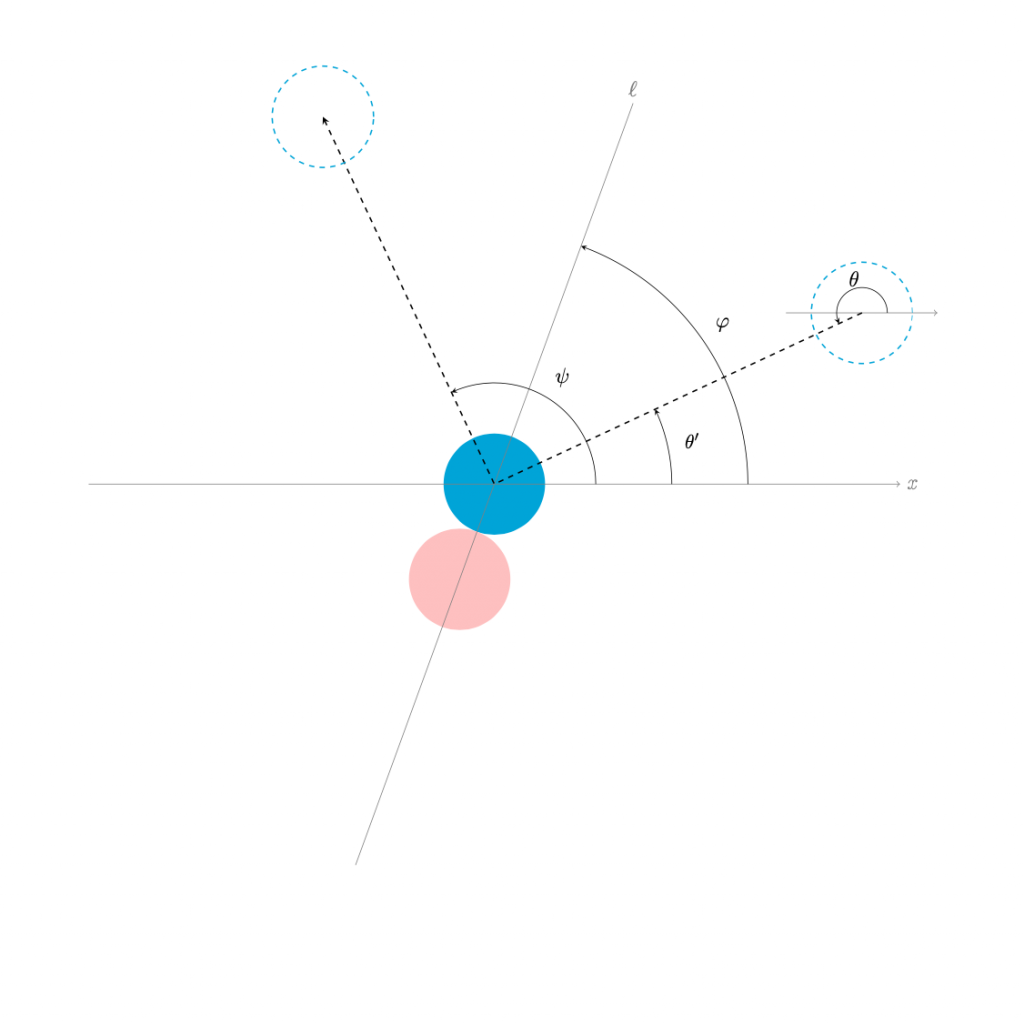
青いボールの軌道を表す点線が，直線$\ell$に関して対称であることに注意すると，等式 $$ \frac{1}{2}(\psi-\theta’)=\varphi-\theta’ $$ が成り立つ．よって， $ \psi=2\varphi-\theta’ $ が従う．

右図のように， $\theta’<0$となる場合でも同様である．

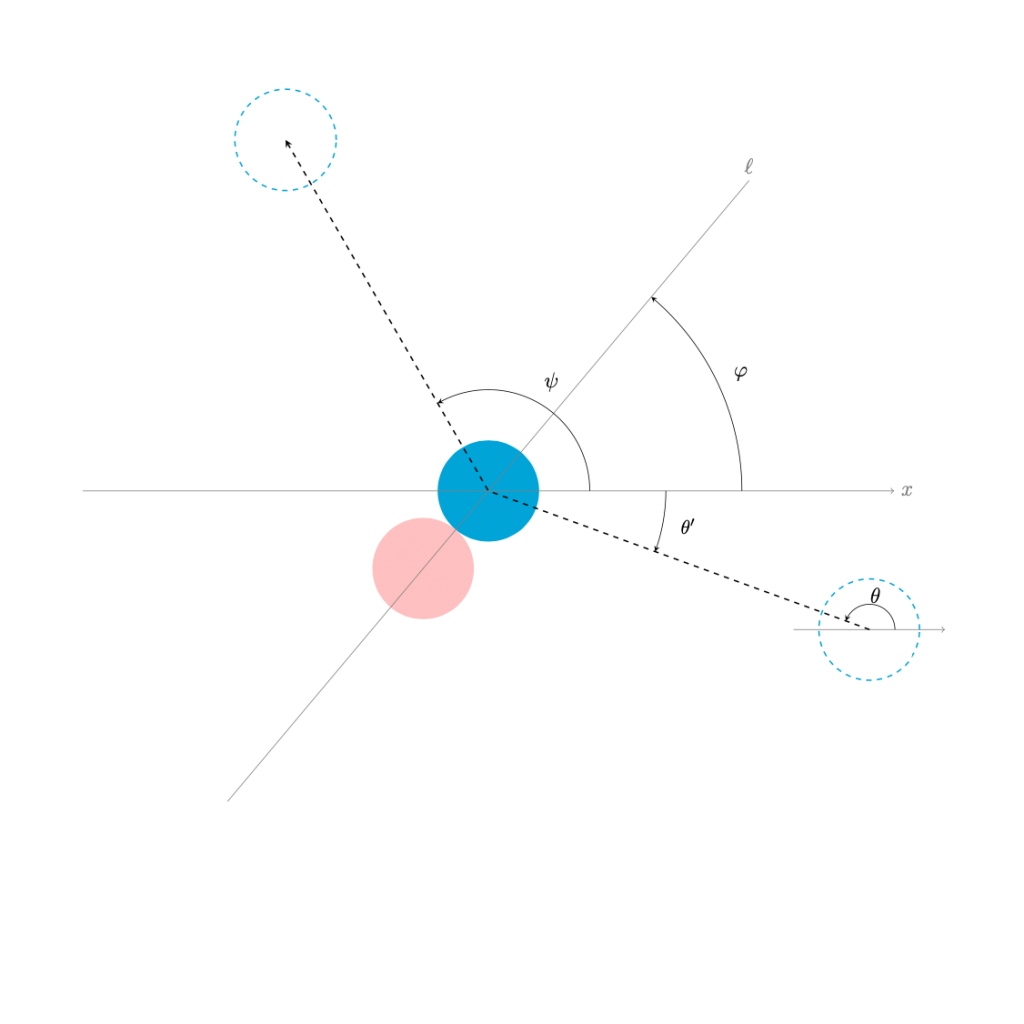
$\varphi<\theta'<\varphi+\frac{\pi}{2}$のとき，

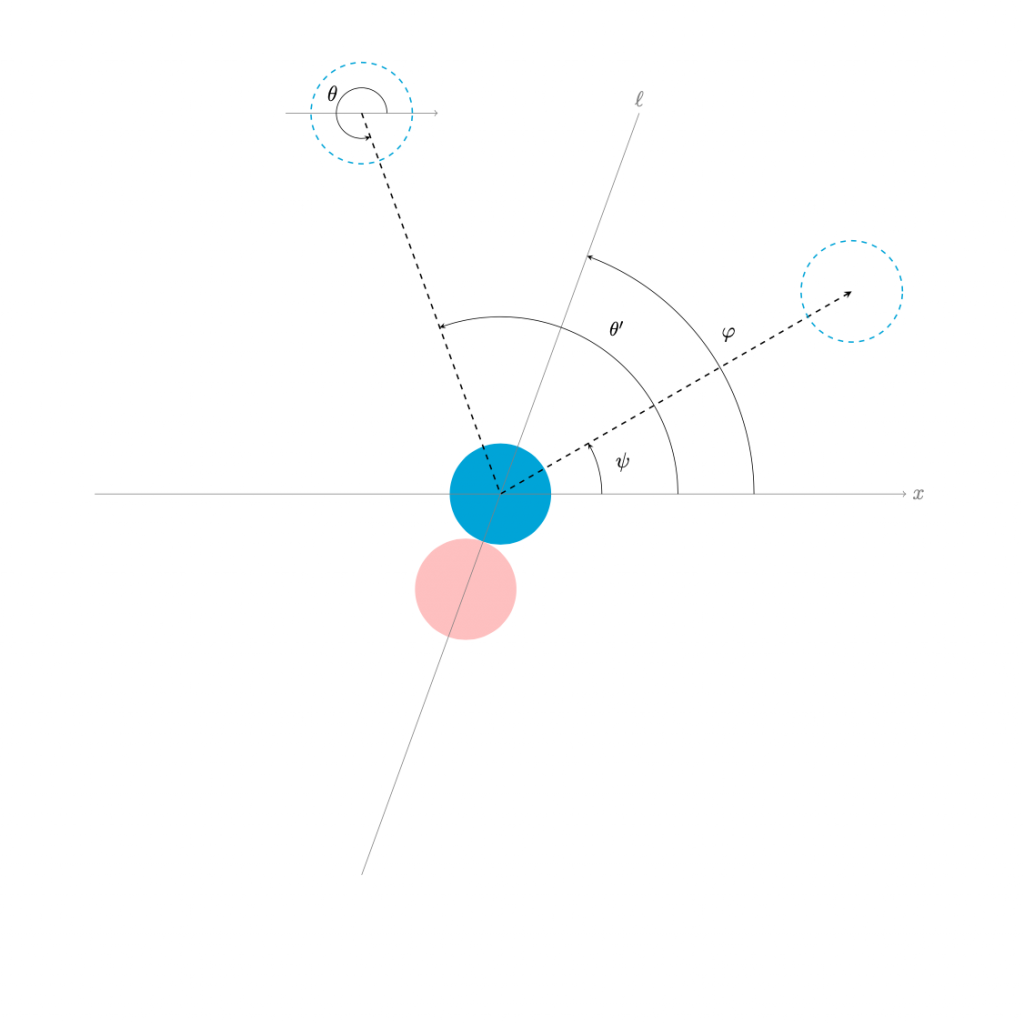
青いボールの軌道を表す点線が，直線$\ell$に関して対称であることに注意すると，等式 $$ \frac{1}{2}(\theta’-\psi)=\varphi-\psi $$ が成り立つ．よって， $ \psi=2\varphi-\theta’ $ が従う．

右図のように， $\psi<0$となる場合でも同様である．

$\theta’ = \varphi$のとき，

青いボールが飛んできた方向と同じ方向に跳ね返る場合である． $$\psi=\theta’=\varphi$$ から， $\psi=2\varphi-\theta’$ が従う．