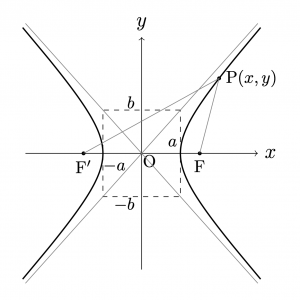
◆焦点が\(x\)軸上にある場
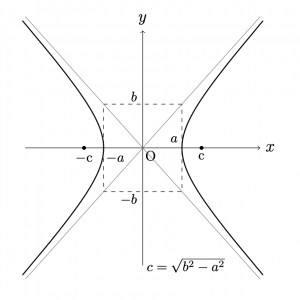
\(c>0\)とする. 2定点\({\rm{F}}(c,0)\),\({\rm{F’}}(-c,0)\) を焦点とし,この2定点からの距離の差が\(2a\)である 双曲線の方程式は, $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$ である.ただし, \(c>a>0\)であり \(b=\sqrt{c^2-a^2}\)とおいた.\((c>b)\)
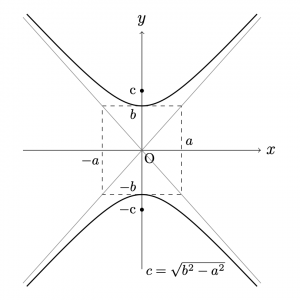
\(c>0\)とする. 2定点\({\rm{F}}(0,c)\),\({\rm{F’}}(0,-c)\) を焦点とし,この2定点からの距離の差が\(2b\)である 双曲線の方程式は, $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$$ である.ただし, \(c>b>0\)であり, \(a=\sqrt{c^2-b^2}\)とおいた.\((c>a)\)
曲線が限りなくある直線に近づくとき, その直線を曲線の漸近線という.
双曲線\(\displaystyle\frac{x^2}{a^2}-\displaystyle\frac{y^2}{b^2}=\pm1 \hspace{5pt}(a>0,b>0)\) の漸近線は,次のようにして求められる:
上の方程式を変形し, \(y^2=\displaystyle\frac{b^2}{a^2}x^2\left(1\mp\displaystyle\frac{a^2}{x^2}\right)\) を得るが,これから, $$y=\pm\displaystyle\frac{b}{a}x\sqrt{1\mp\displaystyle\frac{a^2}{x^2}}$$ が従う. ここで,\(x\)が限りなく大きくなると,\(y\)は,\(\pm\displaystyle\frac{b}{a}x\) に限りなく近づく. よって,2直線\(y=\pm\displaystyle\frac{b}{a}x\) が上の双曲線の漸近線である. これらは,次のようにまとめて書くこともできる.
$$y=\pm\displaystyle\frac{b}{a}x
\hspace{5pt}\Longleftrightarrow\hspace{5pt}
\left(\displaystyle\frac{x}{a}\pm\displaystyle\frac{y}{b}\right)=0
\hspace{5pt}\Longleftrightarrow\hspace{5pt}
\left(\displaystyle\frac{x}{a}+\displaystyle\frac{y}{b}\right)
\left(\displaystyle\frac{x}{a}-\displaystyle\frac{y}{b}\right)=0
\hspace{5pt}\Longleftrightarrow\hspace{5pt}
\displaystyle\frac{x^2}{a^2}-\displaystyle\frac{y^2}{b^2}=0$$
