\(\bullet\)
点\({\rm{P}}\)以外に何も基準がない場合.
(真っ白な紙に点\({\rm{P}}\)だけが描かれている場合.)
基準がないので,位置を表すことができない.
(真っ白な紙に点\({\rm{P}}\)だけが描かれている場合.)
基準がないので,位置を表すことができない.

\(\bullet\)
単位(目盛り)を決め,座標軸を描くことで,
点\({\rm{P}}\)の位置を表すことができる.
注意.
点の位置を表すことができるというのは, 平面上の点と, \(x\)座標と\(y\)座標の組み\((x,y)\)が, 一対一に対応しているからである.
注意.
点の位置を表すことができるというのは, 平面上の点と, \(x\)座標と\(y\)座標の組み\((x,y)\)が, 一対一に対応しているからである.

以上の考察から, 何かしらの基準を作り, 平面上の点と,一対一に対応するものがあれば, それを用いて,平面上の点の位置を表すことができる. すぐ後に見るように,ベクトルを用いて, この一対一対応を作ることができる.
\(\bullet\)
まず,基準となる点\({\rm{O}}\)をとる.
(基準はどこでも良いが,必要である.)
次に,ベクトル\(\overrightarrow{\rm{OP}}\) を考え, $$ \overrightarrow{p}=\overrightarrow{\rm{OP}} $$ とおくと, ベクトル\(\overrightarrow{p}\)を用いて, 点\({\rm{P}}\) の位置を表すことができる.
(基準はどこでも良いが,必要である.)
次に,ベクトル\(\overrightarrow{\rm{OP}}\) を考え, $$ \overrightarrow{p}=\overrightarrow{\rm{OP}} $$ とおくと, ベクトル\(\overrightarrow{p}\)を用いて, 点\({\rm{P}}\) の位置を表すことができる.
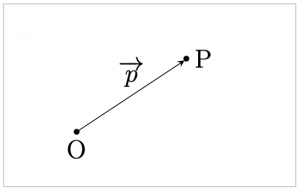
定義. 上で定めた ベクトル\(\overrightarrow{p}\)を (点\({\rm{O}}\)に関する) 点\({\rm{P}}\)の 位置ベクトルという. また点\({\rm{P}}\)の位置ベクトルが, \(\overrightarrow{p}\)であることを, \({\rm{P}}(\overrightarrow{p})\)と表す.
注意. 位置ベクトルを用いて, 平面上の点の位置を表すとき, 基準となる点\({\rm{O}}\)は, (必要であるが,どこでも良いので) 明記されないことが多い.
補足. ここで新しく平面上の点の位置を表す方法を得たのである. これまでの座標を用いた表し方との整合性は次のように確認できる: 座標平面上の点\({\rm{P}}(p,q)\)の位置ベクトルを\(\overrightarrow{p}\)とする. 位置ベクトルの基準となる点\({\rm{O}}\)を, 座標平面上の原点\((0,0)\)にとると, ベクトル\(\overrightarrow{p}\)の成分表示は, $$ \overrightarrow{p}=(p,q) $$である.
次が成り立つ.
平面上の\(2\)点,
\({\rm{A}}(\overrightarrow{a}),\ {\rm{B}}(\overrightarrow{b})\)に対し,
$$
\overrightarrow{\rm{AB}}=\overrightarrow{b}-\overrightarrow{a}.
$$
が成り立つ.
