楕円 – gleamath.com

平面上で，異なる２定点

${\rm{F,F’}}$ からの距離の和が一定である点

${\rm{P}}$ の軌跡を楕円という．２定点

${\rm{F,F’}}$ をその楕円の焦点という．ただし，和

${\rm{PF+PF’}}$ （一定）は，２定点の距離

${\rm{FF’}}$ より大きいとする．

楕円の定義から，次の２つの場合の楕円の方程式を証明する．

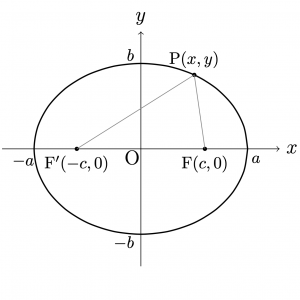
◆焦点が

$x$ 軸上にある場合（横長の楕円）

$c>0$ とする．２定点 ${\rm{F}}(c,0)$ ， ${\rm{F’}}(-c,0)$ を焦点とし，この２定点からの距離の和が $2a$ である楕円の方程式は， $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ である．ただし， $a>c$ であり $b=\sqrt{a^2-c^2}$ とおいた． $(a>b)$

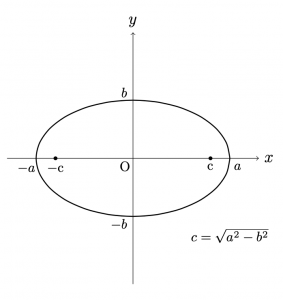
◆焦点が

$y$ 軸上にある場合（縦長の楕円）

$c>0$ とする．２定点 ${\rm{F}}(0,c)$ ， ${\rm{F’}}(0,-c)$ を焦点とし，この２定点からの距離の和が $2b$ である楕円の方程式は， $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ である．ただし， $b>c$ であり， $a=\sqrt{b^2-c^2}$ とおいた． $(b>a)$

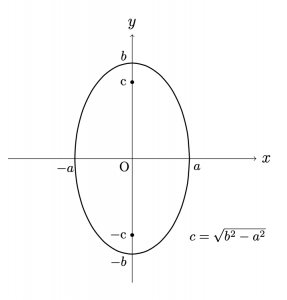
上の２つの楕円の方程式の形が同じであることに気づくだろう．
楕円の方程式が与えられた時に，その楕円が横長なのか縦長なのかを判断するためには，

$a$ と $b$ の大小関係を比較すれば良い．

このような楕円の性質についてまとめた後，楕円の平行移動についても述べる．

PDF