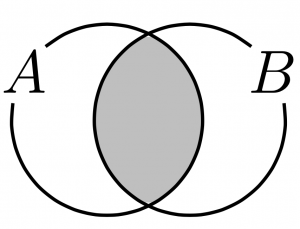
集合\(A,B\)に対して, \(A\)と\(B\)のどちらにも属する要素全体の集合を, \(A\)と\(B\)の共通部分といい, \(A\cap B\)と表す. すなわち, $$A\cap B=\{x\mid x\in A \mbox{かつ} x\in B\}$$ である.
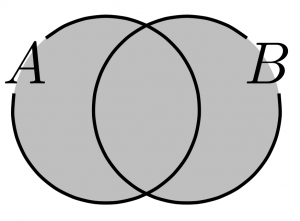
\(A\)と\(B\)の少なくとも一方に属する要素全体の集合を, \(A\)と\(B\)の和集合 といい, \(A\cup B\)と 表す. すなわち, $$A\cup B=\{x\mid x\in A \mbox{または} x\in B\}$$ である.
1つの集合\(U\)を定めて, その部分集合として集合を考えるとき, この\(U\)を全体集合という.
全体集合に対して,次のように補集合というものを定めることができる.全体集合\(U\)の部分集合\(A\)に対して, \(U\)の要素であって, \(A\)の要素ではないもの全体の集合 を \(U\)に関する\(A\)の補集合といい, \(\overline{A}\)と表す. すなわち, $$ \overline{A} =\{x\in U\mid x\not\in A\} $$ である.

\(U\)を全体集合とし, \(A\),\(B\)をその部分集合とするとき, 次が成り立つ.
- \(A\cap \overline{A}=\emptyset\)
- \(A\cup \overline{A}=U\)
- \(\overline{\overline{A}}=A\)
- \(B\subset A\Rightarrow \overline{B}\supset\overline{A}\)
