中線定理
\(\bigtriangleup{\rm{ABC}}\)に対して,
辺\({\rm{BC}}\)の中点を\({\rm{M}}\)とするとき,
次が成り立つ.
$${\rm{AB}}^2+{\rm{AC}}^2=2({\rm{AM}}^2+{\rm{BM}}^2)$$
この式は,
\({\rm{B}}\)と\({\rm{C}}\)に関して対称的な形で書くこともできる.
$$
({\rm{AB}}^2-{\rm{BM}}^2)
+({\rm{AC}}^2-{\rm{CM}}^2)
=2{\rm{AM}}^2
$$
ただし,\({\rm{BM=CM}}\)である.
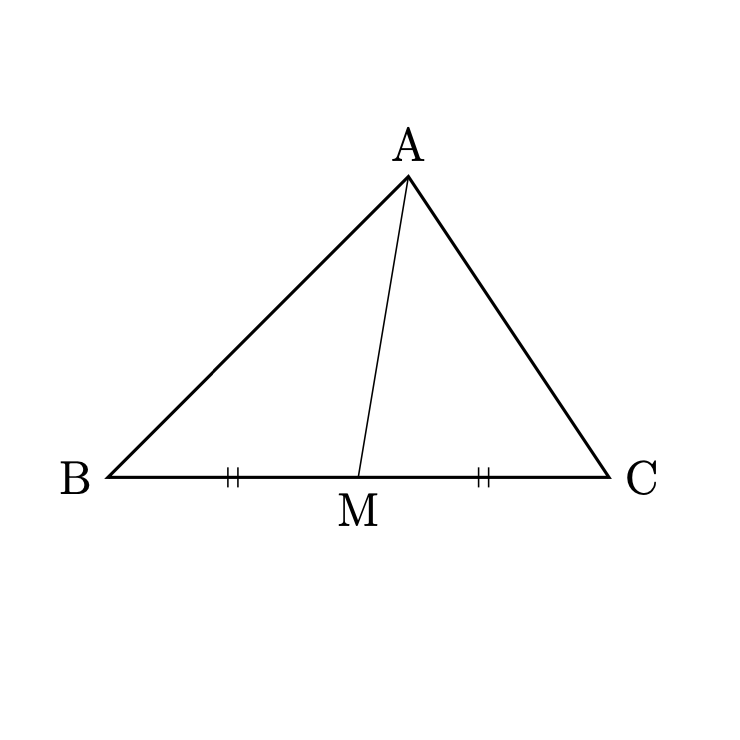
中線定理は,\(\bigtriangleup{\rm{ABC}}\)に対して, 辺\({\rm{BC}}\)を\(1:1\)に内分する点を\({\rm{M}}\)としたときの定理であったが, 内分の比率を一般に\(m:n\)としても同じような結果が成り立つというのが, スチュワートの定理である. スチュワートの定理の結果の式については, 多くの表し方があるが,ここでは中線定理の注意で紹介した形と対応させて定理を述べる.
スチュワートの定理
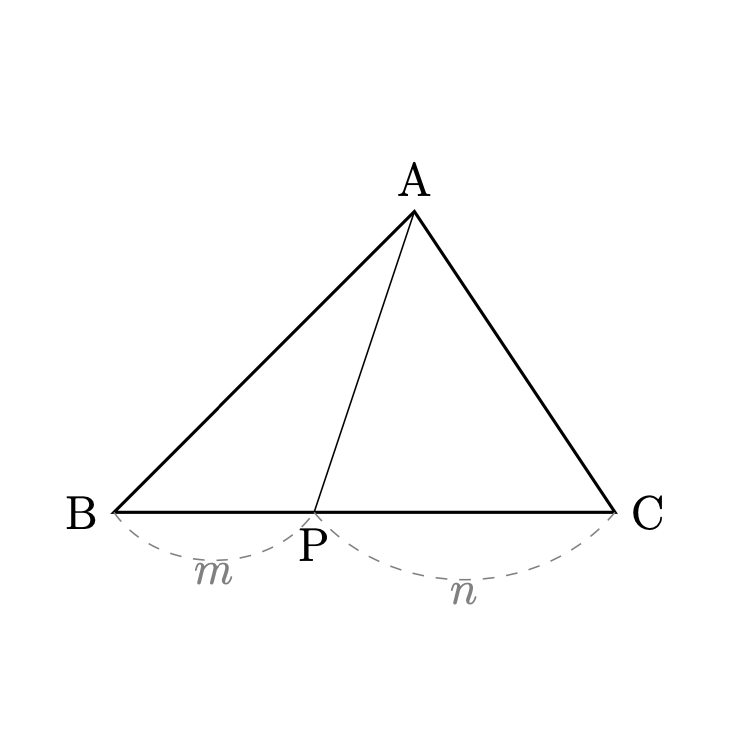
\(\bigtriangleup{\rm{ABC}}\)に対して,
辺\({\rm{BC}}\)を\(m:n\)に内分する点を\({\rm{P}}\)とするとき,
次が成り立つ.
$$
n({\rm{AB}}^2-{\rm{BP}}^2)
+m({\rm{AC}}^2-{\rm{CP}}^2)
=(m+n){\rm{AP}}^2
$$
最後に,スチュワートの定理の系として, 外分点に関する結果を紹介しよう.
\(\bigtriangleup{\rm{ABC}}\)に対して,
辺\({\rm{BC}}\)を\(m:n\)に外分する点を\({\rm{Q}}\)とするとき,
次が成り立つ.
$$
-n({\rm{AB}}^2-{\rm{BQ}}^2)
+m({\rm{AC}}^2-{\rm{CQ}}^2)
=(m-n){\rm{AQ}}^2
$$
