\(\bigtriangleup{\rm{ABC}}\)に対して,
\(\angle{\rm{A}}\)の二等分線と,
辺\({\rm{BC}}\)の交点を\({\rm{P}}\)とする.
このとき,次が成り立つ.
このとき,次が成り立つ.
\( {\rm{AB:AC =BP:PC}} \)
\({\rm{AB\cdot AC -BP\cdot PC=AP^2}} \)
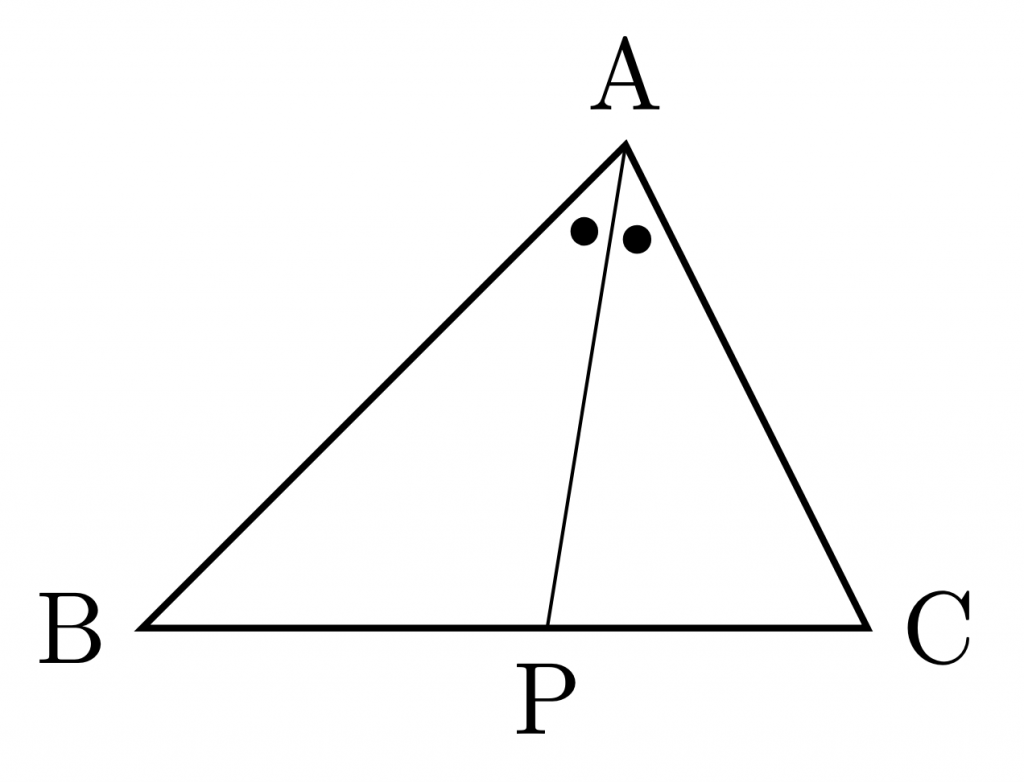
このように, 内角の二等分線から,対辺の内分点が得られることがわかった. 同様に, 外角の二等分線から,対辺の外分点が得られることを証明しよう.
\({\rm{AB\ne AC}}\)である
\(\bigtriangleup{\rm{ABC}}\)に対して,
頂点\({\rm{A}}\)の外角の二等分線と,
辺\({\rm{BC}}\)を延長した直線の交点を\({\rm{Q}}\)とする.
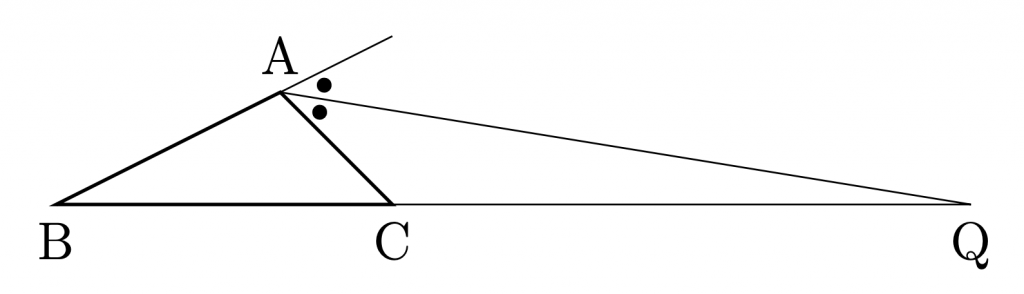
このとき,次が成り立つ.
\( {\rm{AB:AC =BQ:QC}} \)
\( {\rm{AB\cdot AC -BQ\cdot QC=-AQ^2}} \)

どちらの定理も1つ目の主張は, 角の二等分線と平行な補助線を引くとで証明できる. 2つ目の主張には, スチュワートの定理 を用いる.
