問題.
2点\({\rm{A}},\ {\rm{B}}\)に対して,
$$
{\rm{AP:BP}}=m:n
$$
を満たす点\({\rm{P}}\)の軌跡を求めよ.
ただし,\(m,n\)は正の実数とし,\(m\ne n\)であるとする.
補足. 容易にわかるように \(m=n\)の場合,点\({\rm{P}}\)の軌跡は, 線分\({\rm{AB}}\)の垂直二等分線である.
上の問題の軌跡が, 次のようになることを解説する.
解.
線分\({\rm{AB}}\)を\(m^2:n^2\)に外分する点を\({\rm{O}}\)とすると,
点\({\rm{P}}\)の軌跡は,
点\({\rm{O}}\)を中心とする半径\(\sqrt{{\rm{OA\cdot OB}}}\)の円
である. (このような円をアポロニウスの円という.)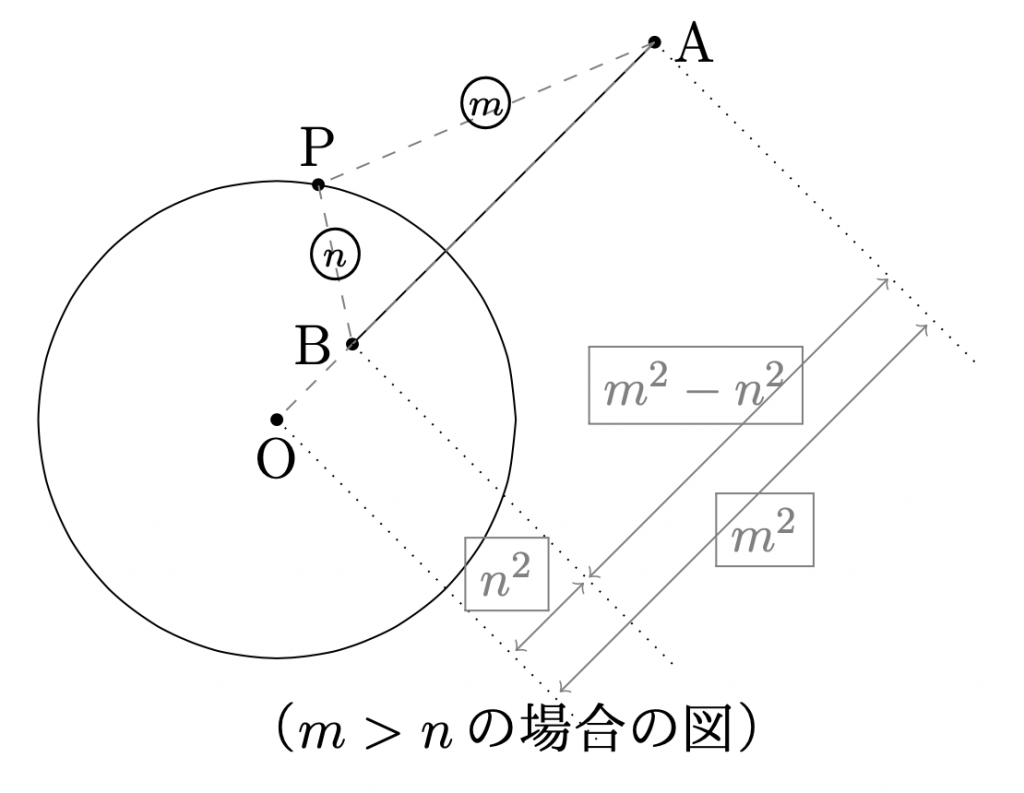
である. (このような円をアポロニウスの円という.)

