命題.\(a > 1,\ b > 0\)とする.
座標平面上において,
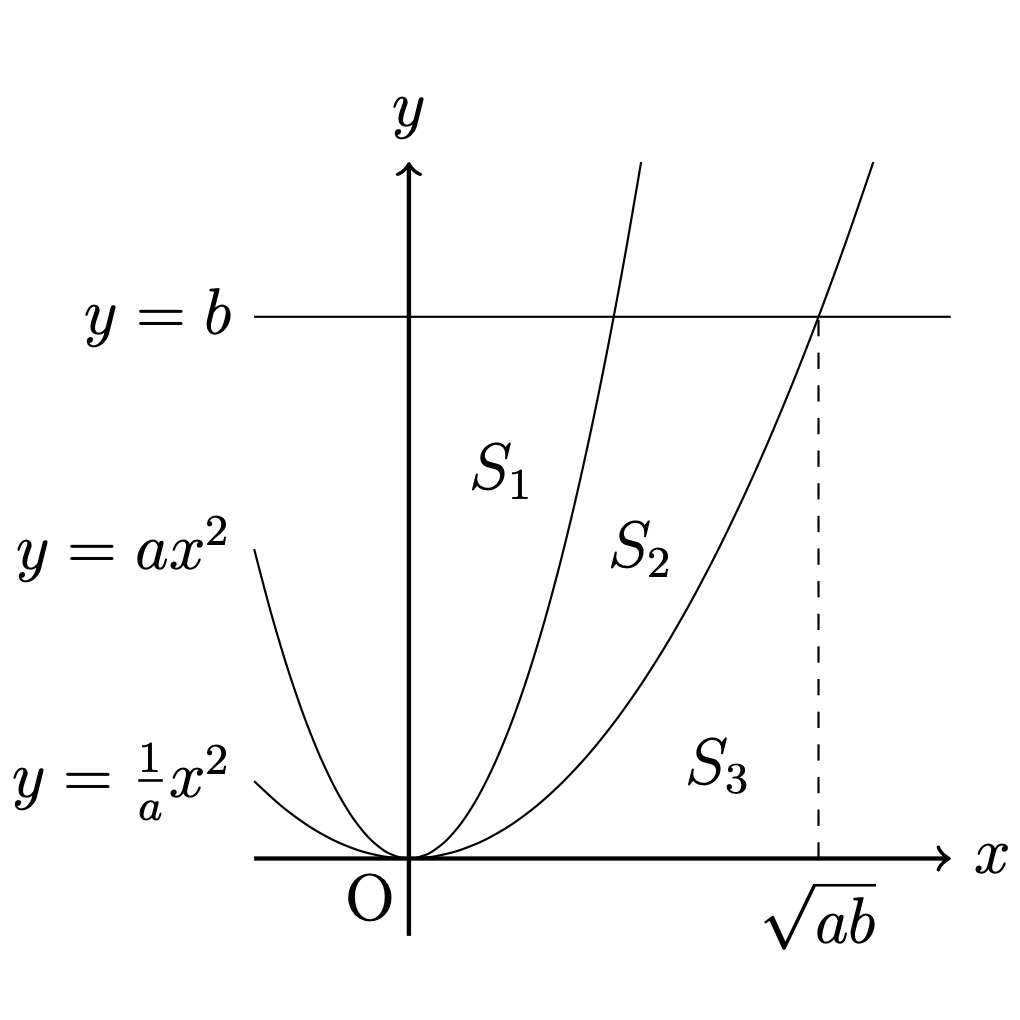
図のように,
\(2\)つの放物線
\(y=ax^2,\ y=\frac{1}{a}x^2\)と,
直線 \(y=b\)で定まる\(3\)つの領域の面積を
それぞれ\(S_1,\ S_2,\ S_3\)とする.このとき,
\(b\)の値によらず,
$$S_1+S_2=2S_3$$
$$S_1:S_2:S_3=2:2(a-1):a$$
が成り立つ.
とくに,
\(a=2\)のときは,
$$
S_1=S_2=S_3.
$$
が成り立つ.