定理.
\(e\)をネイピア数とする.実数\(a, b\)に対して,次が成り立つ.
本稿では,
$$
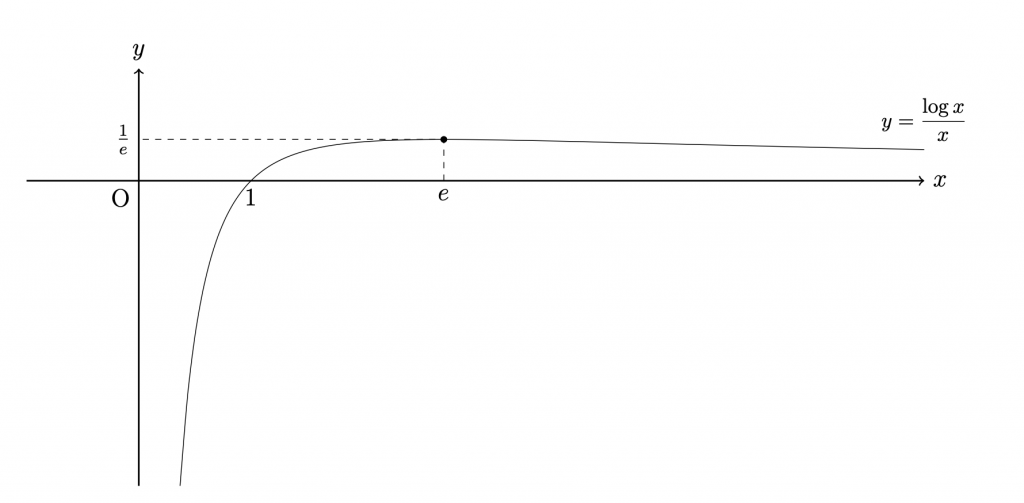
y=\frac{\log x}{x}
$$
のグラフを解析することにより,上の定理を証明する.
グラフの概形が分かれば結果はほとんど明らかである.
- \(e < a < b\)のとき,\(a^b > b^a\),
- \(0 < a < b < e\)のとき,\(a^b < b^a\).