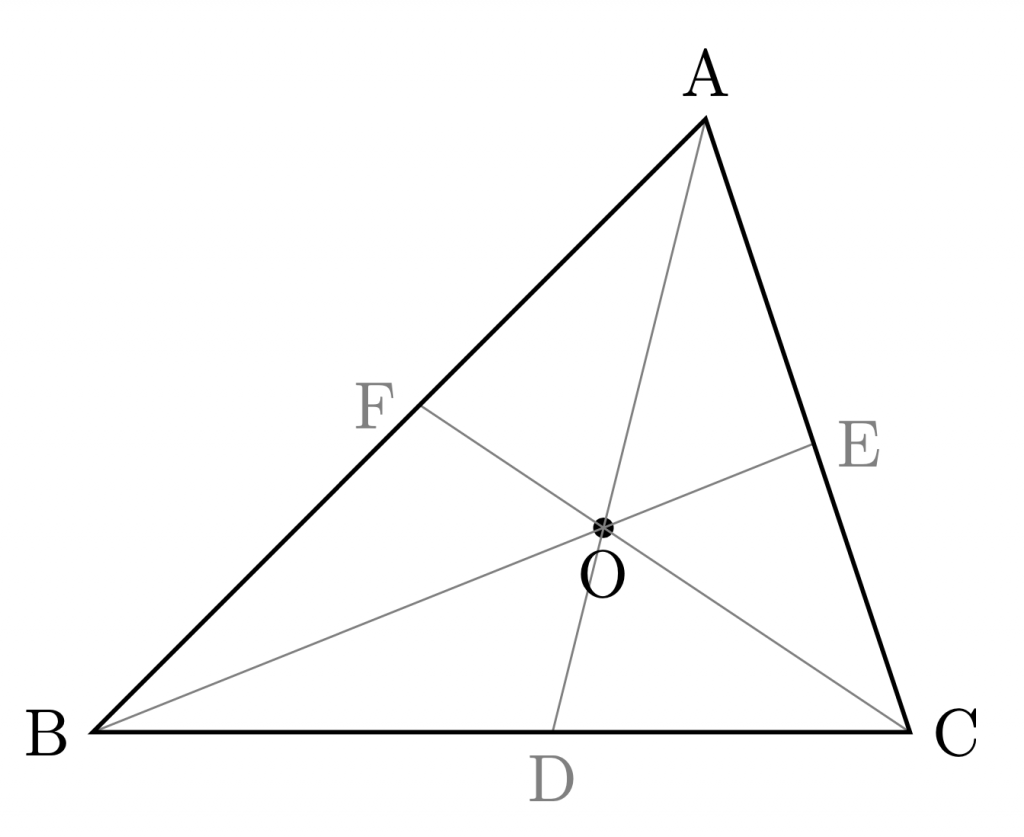
チェバの定理
\(\bigtriangleup{\rm{ABC}}\)と
各辺上またはその延長線上にない点\({\rm{O}}\)に対して,
各頂点\({\rm{A, B, C}}\)から点\({\rm{O}}\)に引いた直線と,
それぞれの対辺(またはその延長線)との交点を\({\rm{D, E, F}}\)とするとき,
次が成り立つ.
$$
\frac{\rm{AF}}{\rm{FB}}
\cdot\frac{\rm{BD}}{\rm{DC}}
\cdot\frac{\rm{CE}}{\rm{EA}}
=1
$$
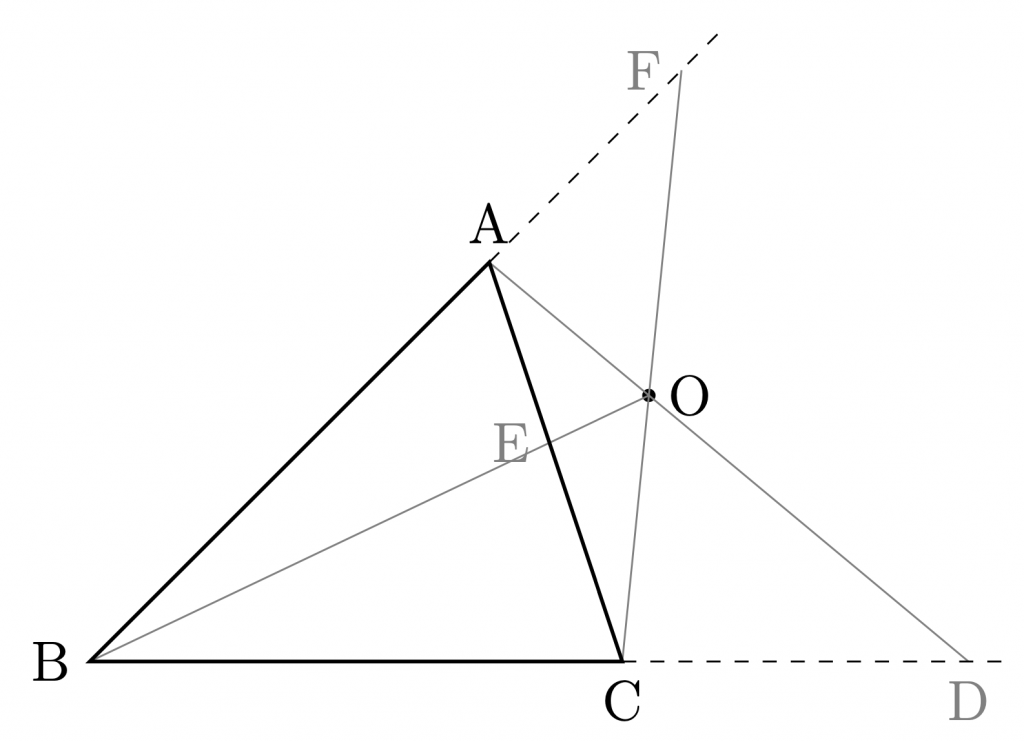


チェバの定理の逆
\(\bigtriangleup{\rm{ABC}}\)において,
- 各頂点\({\rm{A, B, C}}\)の対辺上にある点\({\rm{D, E, F}}\)に対して, $$ \frac{\rm{AF}}{\rm{FB}} \cdot\frac{\rm{BD}}{\rm{DC}} \cdot\frac{\rm{CE}}{\rm{EA}} =1 $$ が成り立つならば, 3直線\({\rm{AD, BE, CF}}\)は1点で交わる.
- 各頂点\({\rm{A, B, C}}\)の対辺または,その延長線上にある 点\({\rm{D, E, F}}\)のうち, 2点が延長線上にあり,もう1点は辺上にあるとする. さらに, 3直線\({\rm{AD, BE, CF}}\)は, どの2直線も互いに平行でないとする. このとき, $$ \frac{\rm{AF}}{\rm{FB}} \cdot\frac{\rm{BD}}{\rm{DC}} \cdot\frac{\rm{CE}}{\rm{EA}} =1 $$ が成り立つならば, 3直線\({\rm{AD, BE, CF}}\)は1点で交わる.
