ベクトルの成分

高校数学By gleamath
座標平面（直交座標）上で， ベクトル を考え， 始点を原点に合わせることによって， その終点の座標は一意的に定まる．
その終点の座標を成分と呼び， 成分にってベクトルを表す方法を成分表示という．
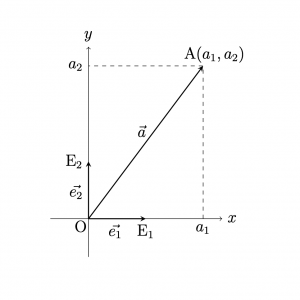
ベクトルの成分表示の定義は， 厳密には基本ベクトルを用いて定義される． （ここで ベクトルの分解定理 が使われることに注意する．）

ベクトルの成分を用いて，その大きさは次のように記述できる．

\(\overrightarrow{a}=(a_1,a_2)\)の大きさは， \(\mid\overrightarrow{a}\mid=\sqrt{a_1^2+a_2^2}\)

また， ベクトルの相等や和・差・実数倍についても， 成分ごとに考えれば良いことがわかる．
  • \((a_1,a_2)=(b_1,b_2)\Longleftrightarrow a_1=b_1,a_2=b_2\)
  • \((a_1,a_2)+(b_1,b_2)=(a_1+b_1,a_2+b_2)\)
  • \((a_1,a_2)-(b_1,b_2)=(a_1-b_1,a_2-b_2)\)
  • \(k(a_1,a_2)=(ka_1,ka_2)\hspace{20pt}(k\in\mathbb{R})\)



PDF