このような方程式でも解を持つように実数の範囲を拡張したいというのが, 虚数を定義する動機である.
2乗して\(-1\)になる数,すなわち\(i^2=-1\)を満たす数\(i\)を 1つ定め,この\(i\)を虚数単位という. また,四則演算は実数と同じようにできる とする.
この虚数単位\(i\)を用いて,複素数を定義する.
\(a,b\)を実数とし, \(i\)を虚数単位とする. このとき,
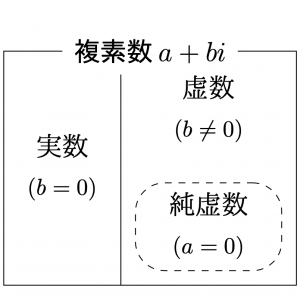
- \(a+bi\)の形で表される数を複素数という.
- 複素数\(a+bi\)のうち,\(b\ne0\)のもの全体を虚数という.
- 虚数\(a+bi\)のうち, \(a=0\)であるものを純虚数という.
- 複素数\(a+bi\)は,\(b=0\)なら,実数である.
次に四則演算に関する次の結果を証明する.
\(a,b,c,d\)を実数とし,\(i\)を虚数単位とする.
2つの複素数\(\alpha=a+bi\),\(\beta=c+di\)の
和・差・積・商はまた複素数であり,
次のようになる.
- [加法] \(\alpha+\beta \hspace{5pt}=\hspace{5pt} (a+bi)+(c+di) \hspace{5pt}=\hspace{5pt} (a+c)+(b+d)i\)
- [減法] \(\alpha-\beta \hspace{5pt}=\hspace{5pt} (a+bi)-(c+di) \hspace{5pt}=\hspace{5pt} (a-c)+(b-d)i\)
- [乗法] \(\alpha\cdot\beta \hspace{8pt}=\hspace{5pt} (a+bi)\cdot(c+di) \hspace{5pt}=\hspace{5pt} (ac-bd)+(ad+bc)i\)
- [除法] \(\displaystyle\frac{\beta}{\alpha} \hspace{10pt}=\hspace{5pt} \displaystyle\frac{c+di}{a+bi} \hspace{10pt}=\hspace{5pt} \displaystyle\frac{(c+di)(a-bi)}{(a+bi)(a-bi)} \hspace{5pt}=\hspace{5pt} \frac{ac+bd}{a^2+b^2}+\frac{ad-bc}{a^2+b^2}i\)
実数変数の二次方程式\(x^2+bx+c=0\)の解は, しばしば,\(0=x^2+bx+c=(x-p)(x-q)\)と因数分解することによって \(x=p,q\)と 求められていたが, ここでは,
$$(x-p)(x-q)=0 \Longleftrightarrow x-p=0 \mbox{ または } x-q=0$$
が成り立つという実数の性質が用いられていたことを思い出す.
次では,複素数にも同様の性質があることを証明する. これにより複素数変数の方程式であっても, 上と同様の方法で解を求めても良いことがわかる.
2つの複素数\(\alpha, \beta\)に対して,
$$\alpha\beta=0\Longleftrightarrow\alpha=0\mbox{ または }\beta=0$$
が成り立つ.
最後に共役複素数を定義し, その性質を証明する.
\(a,b\)を実数,\(i\)を虚数単位とする. 複素数\(\alpha=a+bi\)に対して, 複素数\(a-bi\)(すなわち虚部の符号を反転させたもの)を 共役複素数といい,\(\overline{\alpha}\)で表す. また, 複素数\(\overline{\alpha}=a-bi\)に対しては, 複素数\(\alpha=a+bi\)が共役複素数であるから, \(\alpha\)と\(\overline{\alpha}\)を互いに共役な複素数という.
共役複素数の性質
複素数\(\alpha=a+bi\)と,
その共役複素数\(\overline{\alpha}=a-bi\)に対して,
次が成り立つ.
- \(\alpha+\overline{\alpha}=2a\)
- \(\alpha\cdot\overline{\alpha} =a^2+b^2\)
- \(\overline{\alpha\pm\beta} =\overline{\alpha}\pm\overline{\beta}\)
- \(\overline{\alpha\cdot\beta} =\overline{\alpha}\cdot\overline{\beta}\)
- \(\overline{\left(\displaystyle\frac{\alpha}{\beta}\right)} =\displaystyle\frac{\overline{\alpha}}{\overline{\beta}} \hspace{10pt}(\beta\ne0)\)
- \(\overline{k\alpha} =k\overline{\alpha} \hspace{10pt}(k\in\mathbb{R})\)
