関数\(y=f(x)\)において,
\(x\)が\(a\)から\(b\)まで変化するときの
関数\(f(x)\)の平均変化率
とは,
\(x\)の変化量\(b-a\)に対する,
\(y\)の変化量\(f(b)-f(a)\)の割合のこと,
すなわち
$$\frac{f(b)-f(a)}{b-a}$$
のことである.
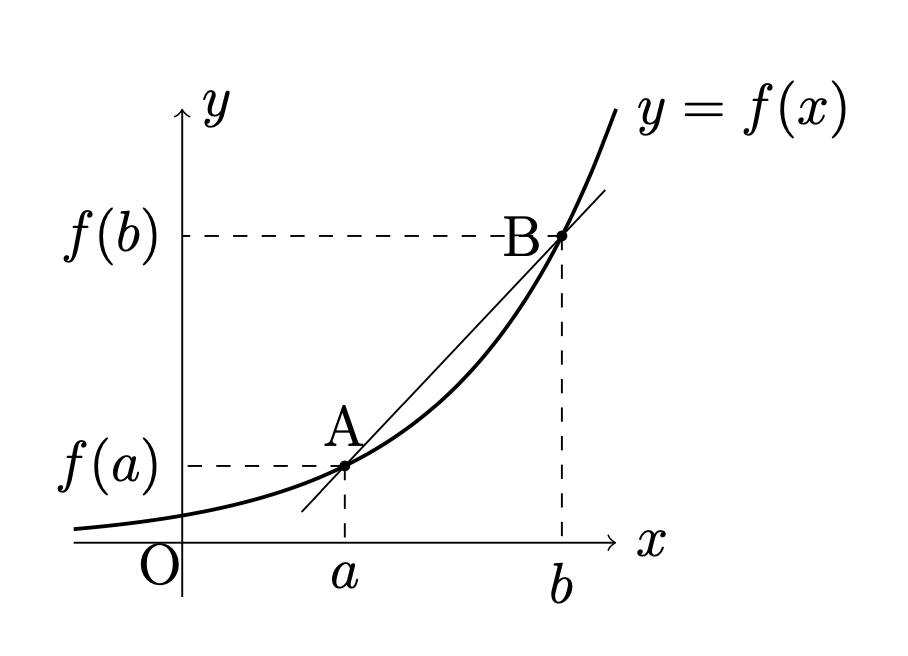
これは,\(y=f(x)\)のグラフ上の
2点
$${\rm{A}}(a,f(a)),\hspace{10pt}{\rm{B}}(b,f(b))$$
を通る直線\({\rm{AB}}\)の傾きである.
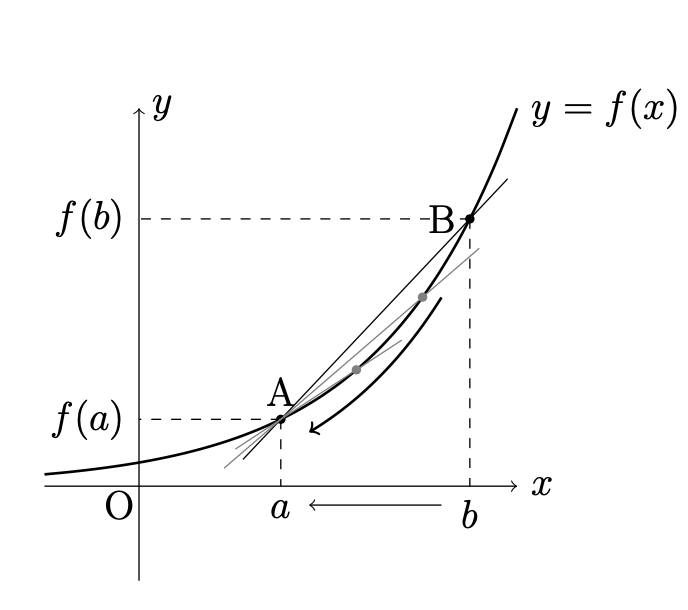
平均変化率は,ある区間\(a\leq x\leq b\) における関数\(f(x)\)の変化の割合であるが, 点\({\rm{B}}\)を点\({\rm{A}}\)に近づけ, この区間を限りなく小さくすることを考える. このときの平均変化率の極限値が存在すれば, それを微分係数という. 正確には,次の定義の通りである.
関数\(f(x)\)において,極限値 $$\lim_{b\to a}\frac{f(b)-f(a)}{b-a}$$ が存在するとき,この値を, 関\(f(x)\)の \(x=a\)における微分係数といい, \(f'(a)\)で表す. これは, \(b-a=h\)とおくことで,次のようにも表せる. $$f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$$
\(f(x)\)において, \(x=a\)における微分係数\(f'(a)\)が存在するとき, \(f(x)\)は\(x=a\)で微分可能であるという.また, 定義域の全ての点で微分可能のときは, 単に, \(f(x)\)は微分可能という.
微分可能性の定義に従って次の定理を証明する.
関数\(f(x)\)が,\(x=a\)で微分可能なら, \(x=a\)で連続である.
導関数を定義する. 関数\(y=f(x)\)が区間\(I\)で微分可能であるとする. このとき,\(a\in I\)に対して,\(f'(a)\)を対応させることで, 新しい関数を定義することができる.すなわち関数
$$I\longrightarrow\mathbb{R}
\hspace{15pt};\hspace{15pt}
a \mapsto f'(a)
$$
を定義することができる.
関数\(y=f(x)\)に対して,上のように定義される関数を \(y=f(x)\)の導関数といい, \(f'(x)\), \(\displaystyle\frac{dy}{dx}\) などと表す.すなわち, $$f'(x) = \lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$$ である. 関数\(f(x)\)から, その導関数を求めることを \(f(x)\)を\(x\)で微分するという.
上でも紹介したように導関数を表す記号はいくつか存在する. これは歴史的な要因が関係している. 記号についての補足をしたのち, 接線と微分の関係 についても述べる.
