定積分と面積

高校数学By gleamath

定積分を用いて，曲線で囲まれる部分の面積を次のように定義できる．

定義． 連続関数\(f(x)\)は，閉区間\([a,b]\)上で，\(f(x)\geq0\)であるとする．このとき，

曲線\(y=f(x)\)，
\(x\)軸（直線\(y=0\)），
直線\(x=a\)，
直線\(x=b\)

で囲まれる部分の面積\(S\)を $$ S=\int_a^b f(x)\, dx $$ と定める．

この定義と，次の性質

図形を分割したとき，分割してできた図形の面積の和は，もとの図形の面積と等しい．
合同な図形の面積は等しい．

を認めることにより，次のような，２曲線で挟まれる部分の面積も求めることができる．

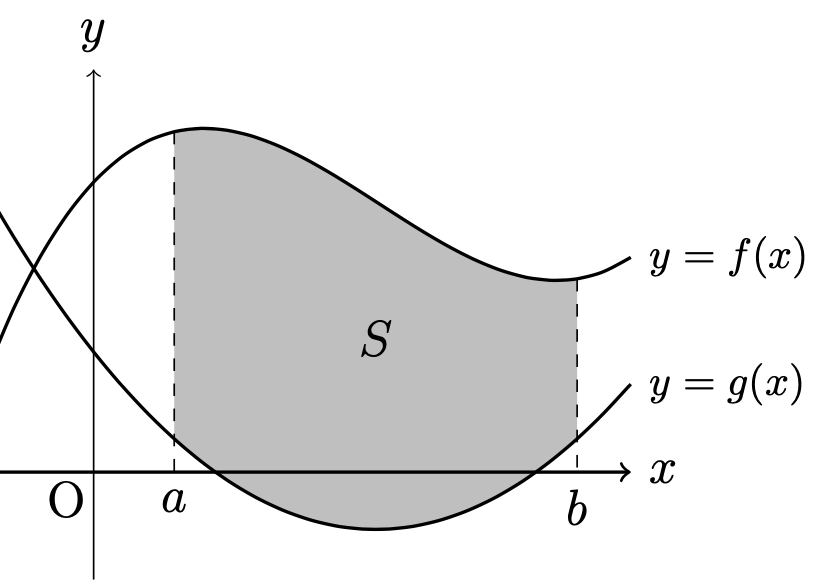
命題． 連続関数\(f(x),\ g(x)\)は，閉区間\([a,b]\)上で，\(f(x)\geq g(x)\)であるとする．このとき，

曲線\(y=f(x)\)，
曲線\(y=g(x)\)，
直線\(x=a\)，
直線\(x=b\)

で囲まれる部分の面積を\(S\) とすると， $$ S=\int_a^b \{f(x)-g(x)\}\, dx $$ が成り立つ．

PDF