内分点と外分点

線分\({\rm{AB}}\)の中点\({\rm{M}}\)とは， 線分\({\rm{AB}}\)を半分に分ける点，すなわち \({\rm{AM}}={\rm{BM}}\)が成り立つような， 線分\({\rm{AB}}\)上の点のことであった． \({\rm{AM}}={\rm{BM}}\)が成り立つとは， 辺の比を使って言い換えると， \({\rm{AM}}:{\rm{BM}}=1:1\)が成り立つということであるが， ここでは，もっと一般の比に対して， 線分\({\rm{AB}}\)を分ける点を定義する．

以下，\(m,n\)は正の数とする．

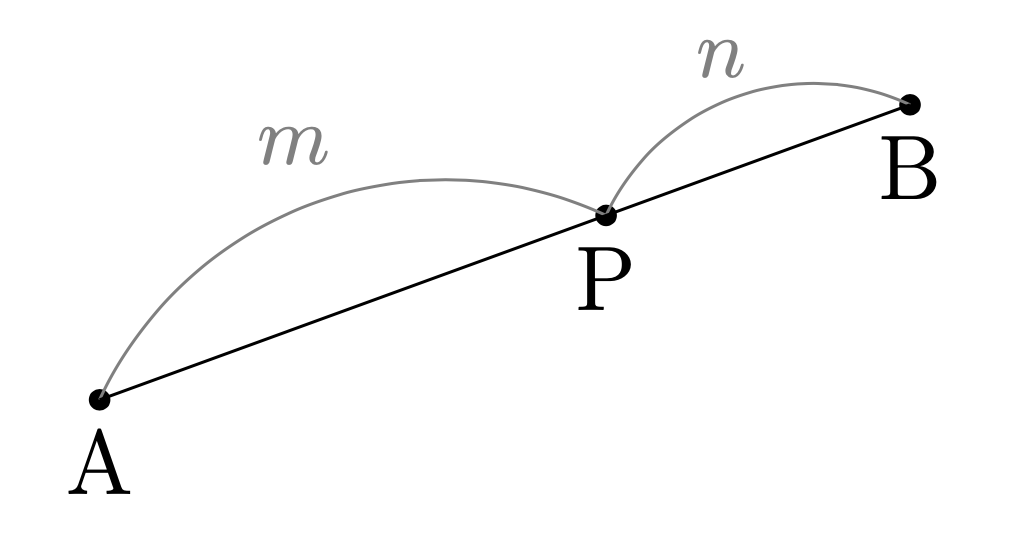
線分\({\rm{AB}}\)を\(m:n\)に内分する点\({\rm{P}}\)とは， $${\rm{AP}}:{\rm{PB}}=m:n$$ が成り立つような， 線分\({\rm{AB}}\)上の点のことをいう． 点\({\rm{P}}\)のことを 内分点ともいう．

さらに， 線分\({\rm{AB}}\)の延長線上にある点に対しても次のように定義する．

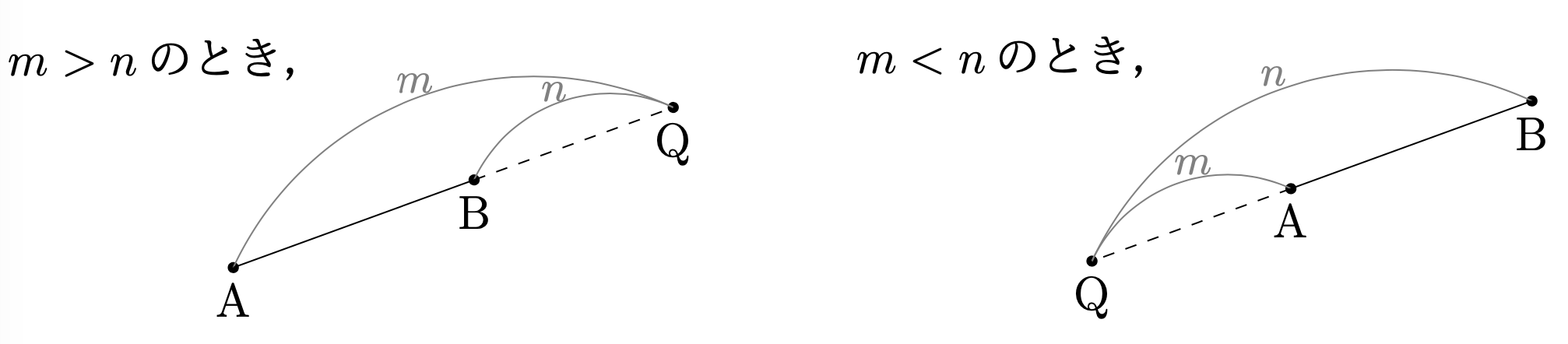
\(m\ne n\)とする． 線分\({\rm{AB}}\)を\(m:n\)に外分する点\({\rm{Q}}\)とは， $${\rm{AQ}}:{\rm{QB}}=m:n$$ が成り立つような， 線分\({\rm{AB}}\)の延長線上にある点のことをいう． 点\({\rm{Q}}\)のことを 外分点ともいう．

内分点は，線分\({\rm{AB}}\)上の点であったのに対して， 外分点は，線分\({\rm{AB}}\)の延長線上にある点 （線分\({\rm{AB}}\)上の点ではない） であることに注意する．また， 外分点は，\(m\)と\(n\)の大小により， 線分\({\rm{AB}}\)の延長線上の\({\rm{A}}\)側にあるか， \({\rm{B}}\)側にあるかが変わるので注意する


PDF