\(4\)次関数 の複接線の存在条件について,次が成り立つ.
命題.
\(f(x)=ax^4+bx^3+cx^2+dx+e\ (a\ne0)\)とする.
曲線\(C:y=f(x)\)の複接線\(\ell\)が存在するための必要十分条件は,
\(2\)次導関数\(f^{\prime\prime}(x)\)に対して,
\(f^{\prime\prime}(x)=0\)が異なる\(2\)つの実数解
を持つこと,
すなわち,
$$
3b^2-8ac>0
$$
が成り立つことである.
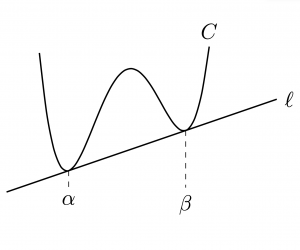

注意. (\(4\)次関数とは限らない)一般の曲線\(C:y=f(x)\)に対しても,
\(C\)が複接線を持つための 必要条件は,\(f^{\prime\prime}(x)=0\)が異なる\(2\)つの解を持つことである
