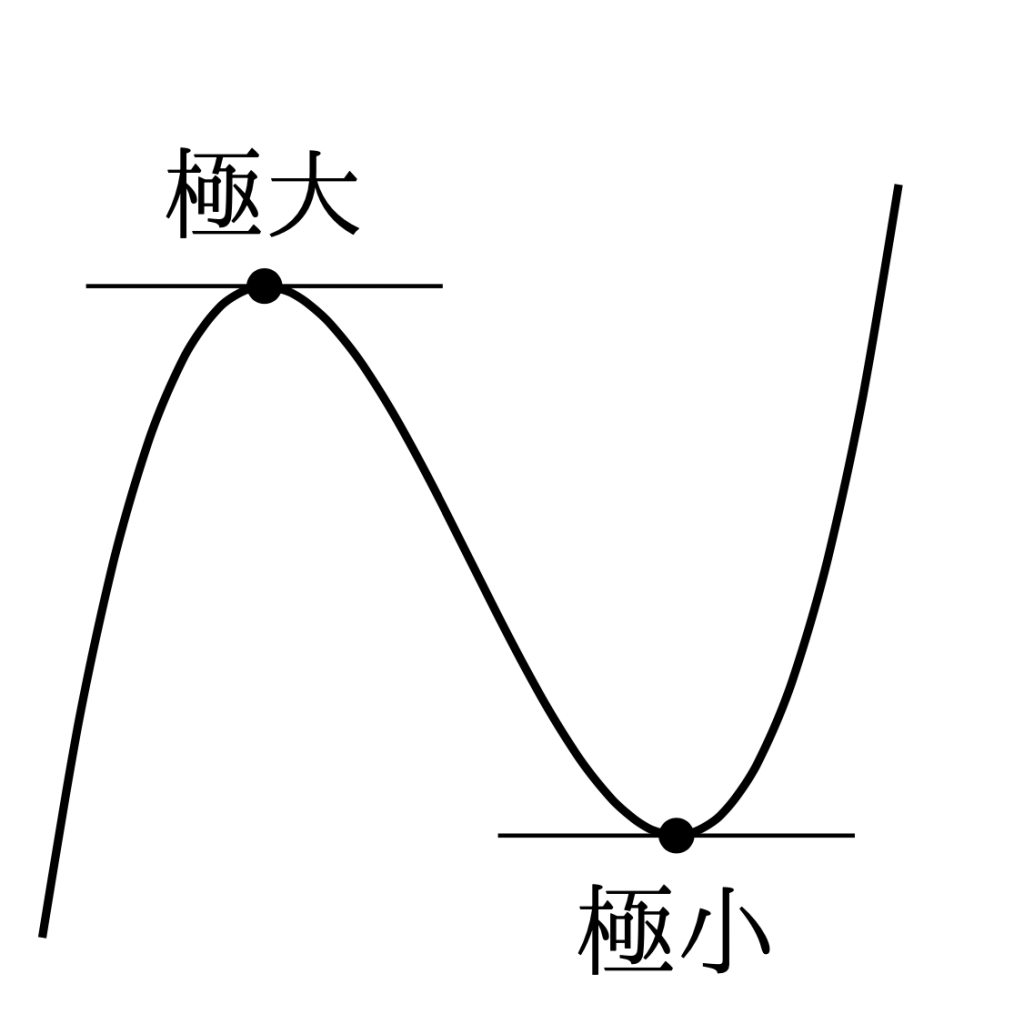
定義. 連続関数\(y=f(x)\)について, \(x=a\)の十分近くの点\((x\ne a)\)で,
- \(f(x) < f(a)\)が成り立つとき, \(f(x)\)は\(x=a\)で極大であるといい, \(f(a)\)を極大値という.
- \(f(x) > f(a)\)が成り立つとき, \(f(x)\)は\(x=a\)で極小であるといい, \(f(a)\)を極小値という.
極値の定義から,次が成り立つ.
微分可能な関数\(f(x)\)において,次が成り立つ.
\(f(a)\)が極値 \(\Longrightarrow\) \(f'(a)=0\)
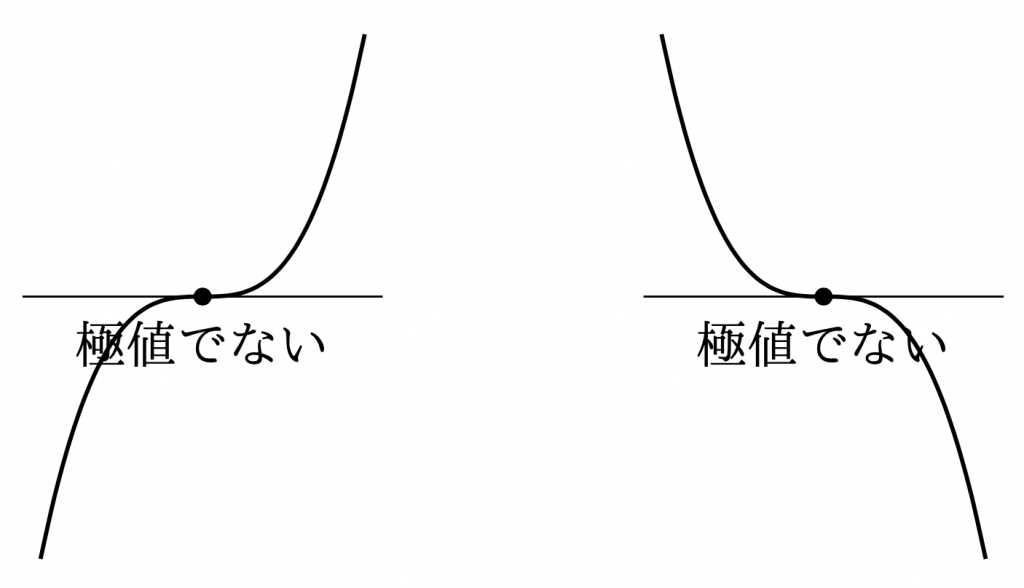
注意. 上の命題の逆は成り立たない. すなわち,\(f'(a)=0\)であっても, \(f(a)\)が極値であるとは限らないことに注意する.