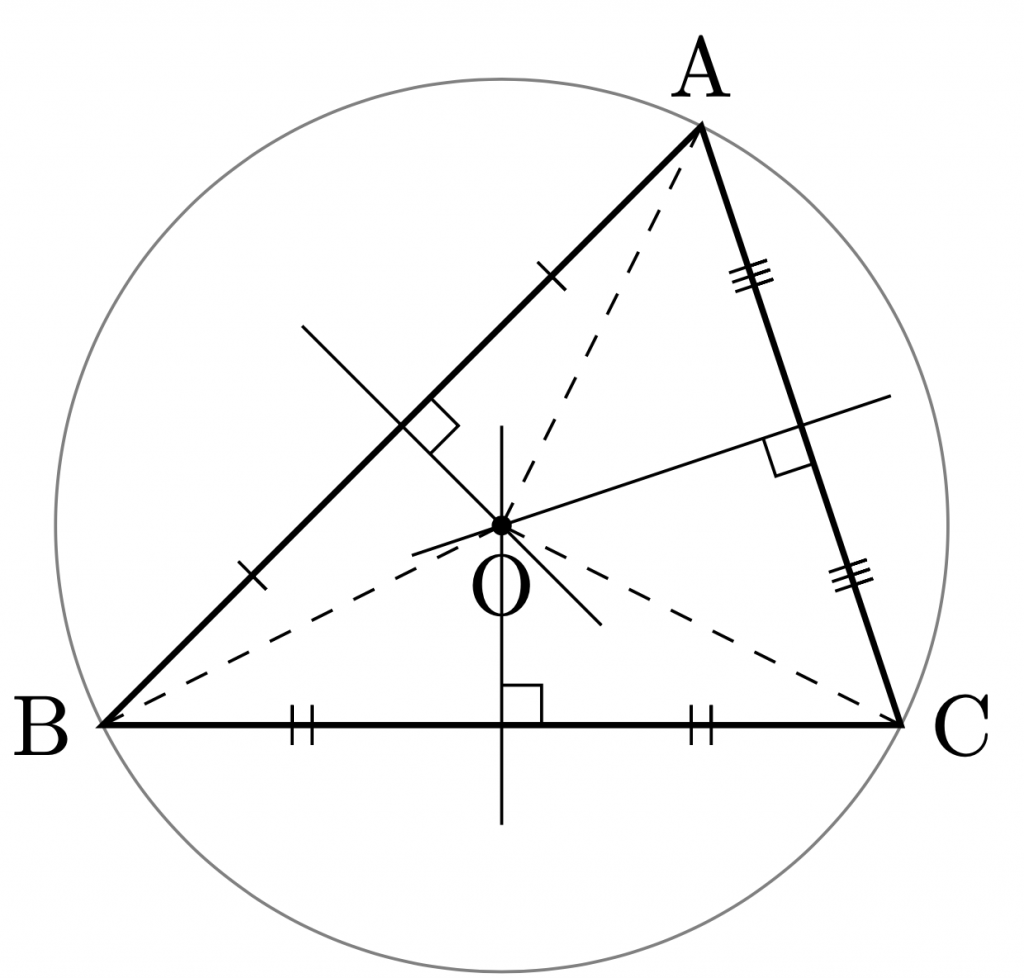
3つの辺の垂直二等分線.
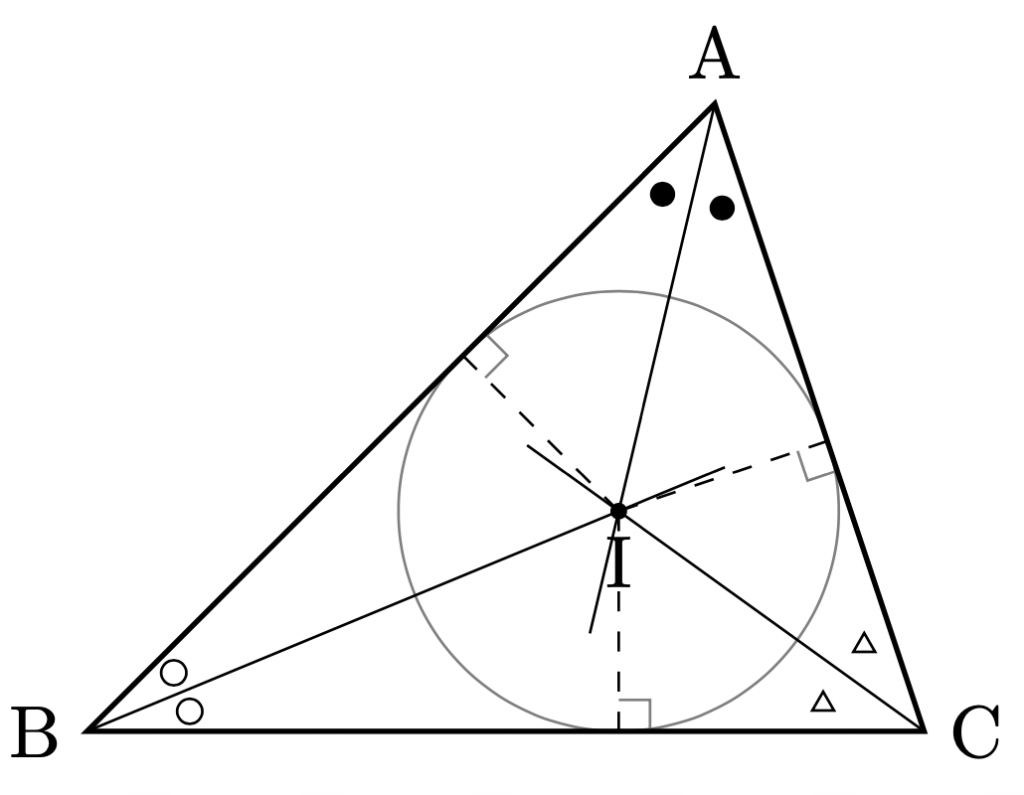
3つの内角の二等分線.
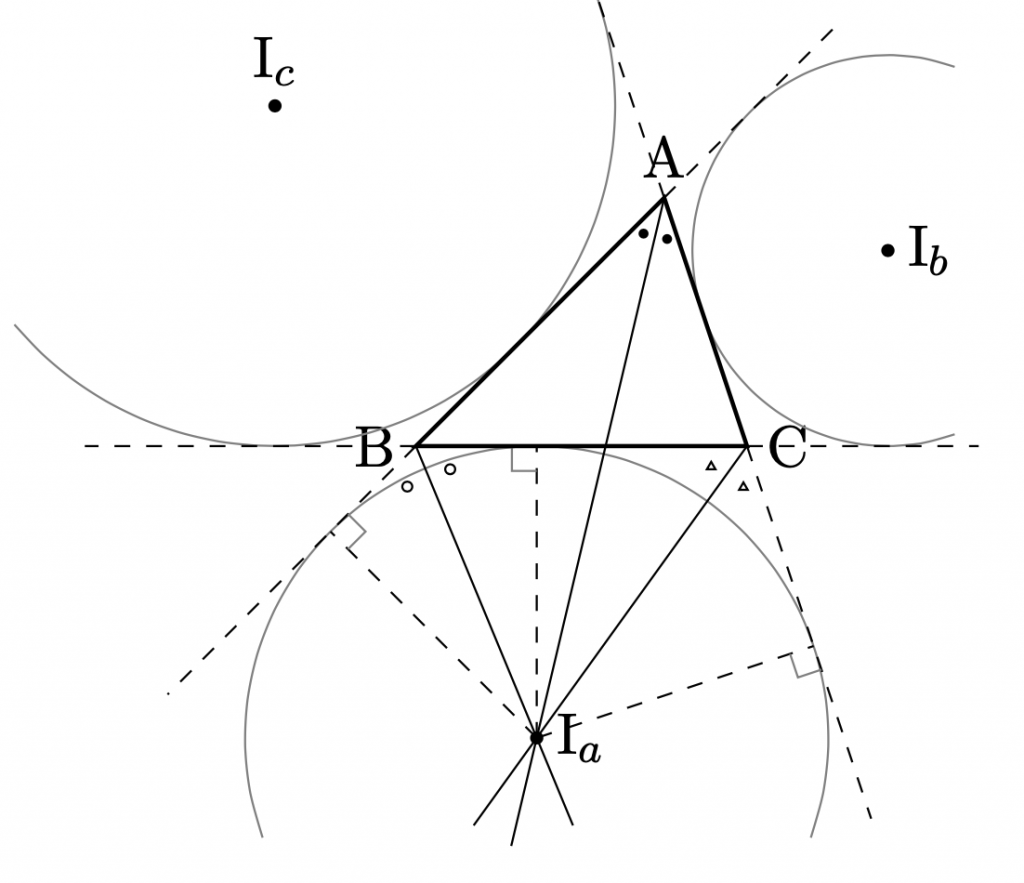
1つの頂点の内角の二等分線と,他の2つの外角の二等分線.
3本の中線(頂点から対辺の中点に引いた線).
3頂点から,対辺(またはその延長線)に下ろした垂線.
上の定理における交点は次のように呼ばれる.
三角形において,
3つの辺の垂直二等分線の交点を外心という.
3つの内角の二等分線の交点を内心という.
1つの頂点の内角の二等分線と,他の2つの外角の二等分線の交点を傍心という.
3本の中線の交点を重心という.
3頂点から,対辺(またはその延長線)に下ろした垂線の交点を垂心という.
次に五心の基本的な性質を紹介する.
定理. 三角形において,
外心は,3頂点から等距離にある.
内心は,3辺から等距離にある.
傍心は,1つの辺と他の2辺の延長線から等距離にある.
三角形の重心は,各中線を(頂点から)\(2:1\)に内分する.
上の定理から,次のように,外心,内心,傍心を中心とする円を定義できる.
三角形において,
ここでは,上で述べた事実のうち,
外心を中心として,3頂点を通る円を,外接円という.
内心を中心として,3辺に接する円を,内接円という.
傍心を中心として,1つの辺と他の2辺の延長線に接する円を,傍接円という.
外心・内心・傍心
外心\({\rm{O}}\)と外接円
内心\({\rm{I}}\)と内接円
傍心と傍接円