定義.
微分可能な関数\(y=f(x)\)と,
その定義域内の区間\(I\)に対して,
任意の\(u, v\in I\ (u < v)\)をとる.
- 曲線\(y=f(x)\)が, 区間\(I\)で下に凸であるとは, 次が成り立つときをいう. $$ u< x < v \ \Longrightarrow \ \frac{f(x)-f(u)}{x-u} \leq \frac{f(v)-f(x)}{v-x} $$
- 曲線\(y=f(x)\)が, 区間\(I\)で上に凸であるとは, 次が成り立つときをいう. $$ u< x < v \ \Longrightarrow \ \frac{f(x)-f(u)}{x-u} \geq \frac{f(v)-f(x)}{v-x} $$
上で定義した下に凸や上に凸は, 直感的には,下図のようなことを言っている.
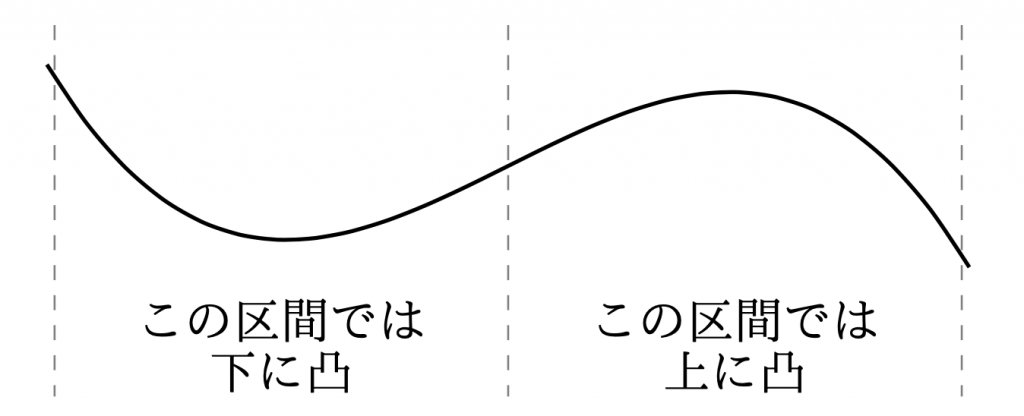
任意の\(u, v\in I\ (u < v)\)をとり, 2点\({\rm{U, V}}\)を, $${\rm{U}}(u,f(u)),\ {\rm{V}}(v,f(v))$$ と定める. このとき, 次の命題を証明する.
命題.
\(y=f(x)\)が,
区間\(I\)で下に凸であるとは,
次と同値である.
- 任意の区間\([u,v]\)上で, 曲線\(y=f(x)\)は,線分\({\rm{UV}}\)の下側にある.
- 接線の傾きが単調に増加する. すなわち,導関数\(f'(x)\)は, \(I\)上で単調増加である.
- \(I\)上における接線は, 常に曲線\(y=f(x)\)の下側にある.
