指数関数の定義域は実数全体とする.
指数関数のグラフは,底\(a\)の値に注意して, 次のように描くことができる.
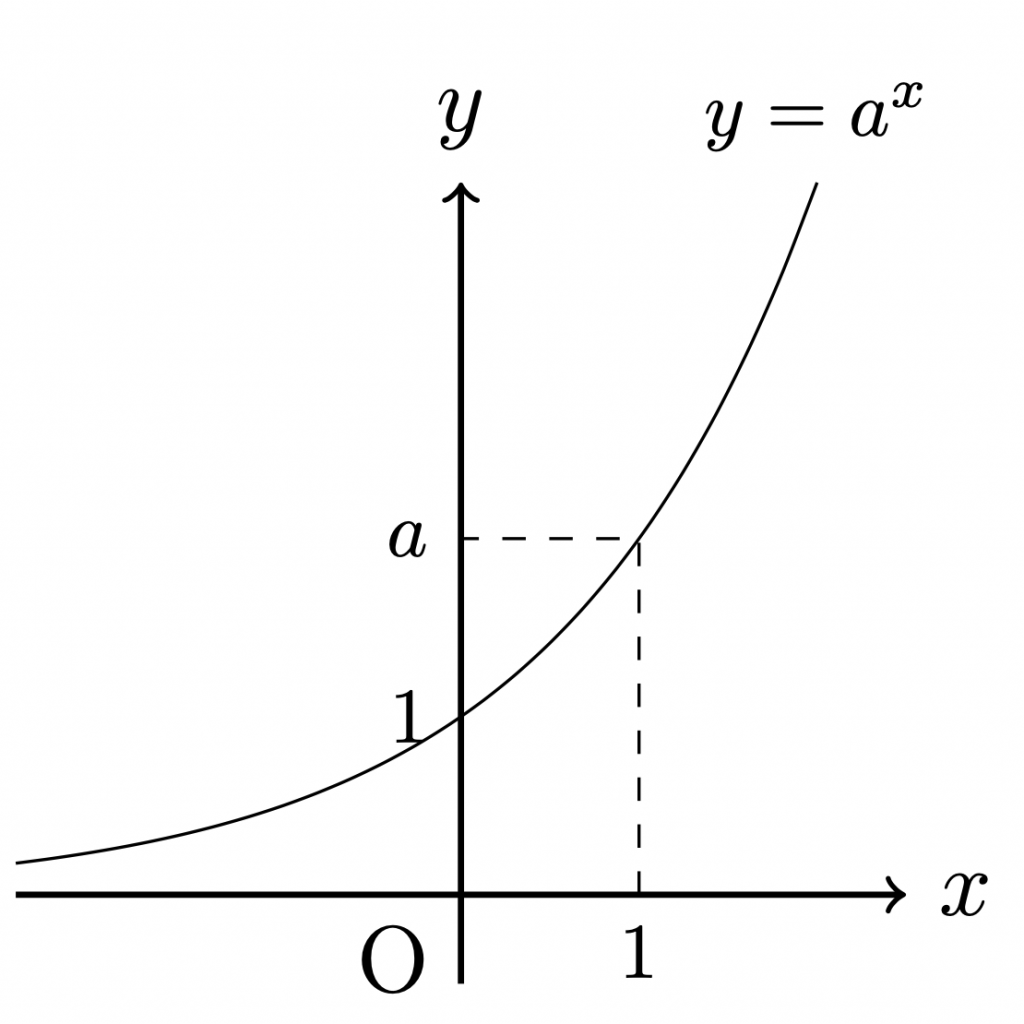
\(a > 1\)のとき,

\(0 < a < 1\)のとき,
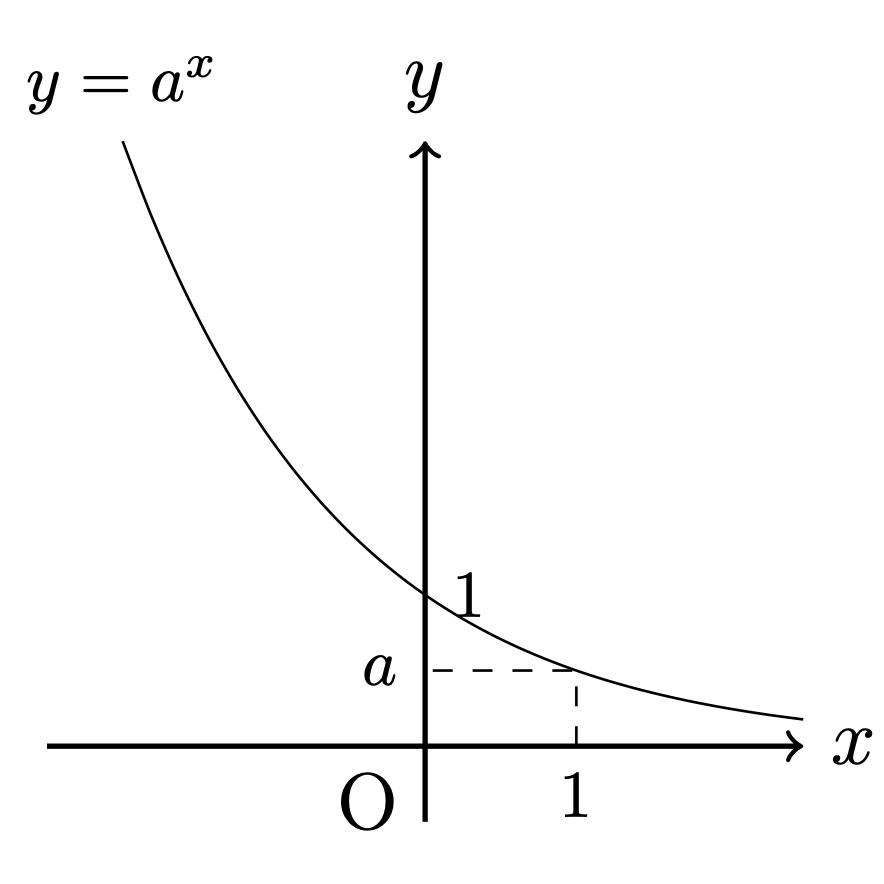

指数関数\(y=a^x\)について,次が成り立つ.
- 値域は正の実数全体である.
- \(a > 1\)のとき単調増加であり, \(0 < a < 1\)のとき単調減少である.
- グラフは点\((0,1)\)を通る.
- \(x\)軸はグラフの漸近線である.
最後に,グラフの対称性や平行移動についても 次のような例を用いて説明する.
- \(y=5^x\)のグラフと, \(y=\left(\displaystyle\frac{1}{5}\right)^x\)のグラフは, \(y\)軸に関して対称である.
- \(y=\displaystyle\frac{2^x}{8}\)のグラフは, \(y=2^x\)のグラフを\(x\)軸方向に\(3\)だけ平行移動したグラフである.
