- 数列をある規則に従って いくつかの組に分けるとき, この組の列を 群数列という.
- \(1,2,\cdots\)番目の組を それぞれ, 第1群,第2群,\(\cdots\)いう.
- 第\(n\)群に含まれる(元の)数列の項のうち, 最後の項を 第\(n\)群の末項という.
- 第\(n\)群に含まれる(元の)数列の項のうち, 初めの項を 第\(n\)群の初項という.
- 第\(n\)群に含まれる(元の)数列の項の数を, 第\(n\)群の項数という.
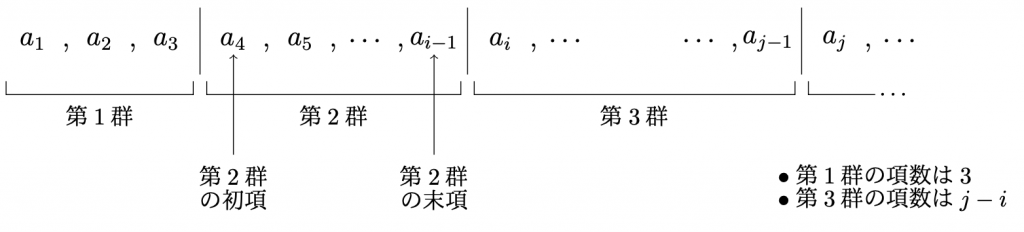
数列\(\{a_n\}_{n=1}^\infty\)をいくつかの組に分け,群数列を考える. この群数列の第\(n\)群の項数を\(m_n\), として,数列\(\{m_n\}_{n=1}^\infty\)を定める. このとき, 第\(k\)群の初項は, 数列\(\{a_n\}_{n=1}^\infty\)の第 \(\displaystyle\sum_{i=1}^{k-1} m_i+1\) 項 の数である. すなわち, 各群の初項を並べた数列は,
$$
\{a_{n_k}\}_{k=1}^\infty
,\hspace{20pt}
n_k = \sum_{i=1}^{k-1} m_i+1
$$
と表すことができる.
このとき, 数列\(\{a_{n_k}\}_{k=1}^\infty\)がどのような数列になるのかを考察する.
結論は次の通りである.

