まずは,実数から実数への関数 $$f:\mathbb{R}\longrightarrow\mathbb{R} \hspace{2pt};\hspace{2pt} x \mapsto y=f(x)$$ について復習する. 特に, \(y=f(x)\)のグラフとは, 関数\(f\)の定義域\(\mathbb{R}\) と値域\(\mathbb{R}\)を合わせた 平面上に描かれることに注意する.
表題のように,虚数解を考えたいので, 関数\(f\)の定義域を複素数全体\(\mathbb{C}\)に拡張する必要が, 定義域を複素数全体\(\mathbb{C}\)まで拡張してしまうと, 多くの場合,値域も複素数全体\(\mathbb{C}\)となってしまう. 複素数全体\(\mathbb{C}\)は, $$\mathbb{C}\longrightarrow\mathbb{R}^2 \hspace{2pt};\hspace{2pt} x_1+ix_2 \mapsto (x_1,x_2) $$ という対応により,平面\(\mathbb{R}^2\)と同一視できるが, そうするとグラフを描く際に, 定義域\(\mathbb{C}\)と値域\(\mathbb{C}\)を合わせた 4次元空間を考えることになってしまうので,都合が悪い.
しかし,虚数解を考えるだけであれば, 値域は\(\mathbb{R}\)で十分なので, \(f(x)\)に対して,\(\mathbb{C}\)の部分集合 $$A_f:=\{x\in\mathbb{C}\mid f(x)\in\mathbb{R}\}$$ を考え, \(A_f\)を定義域とする関数 $$f:A_f\longrightarrow\mathbb{R} \hspace{2pt};\hspace{2pt} x \mapsto y=f(x)$$ を考える. これにより, 定義域\(A_f\)と,値域\(\mathbb{R}\)を合わせた 3次元空間にグラフを描くことができる.
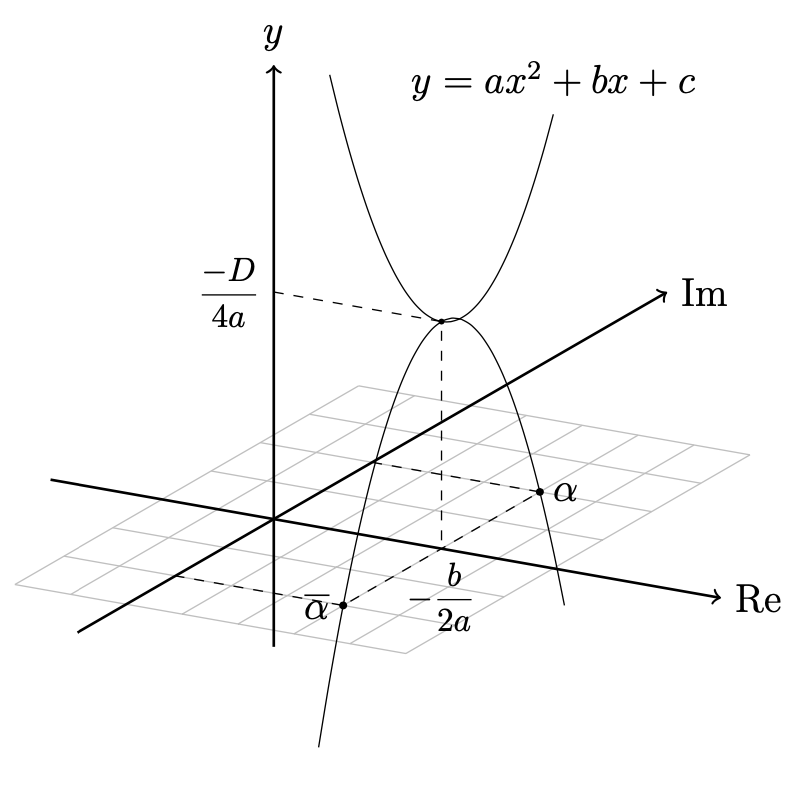
結果的に,\(y=f(x)\)のグラフは, 下図のようになることを証明する.