\(\overrightarrow{a}\)と, \(\overrightarrow{b}\)の\(\overrightarrow{a}\)への正射影ベクトル の符号付き長さの積
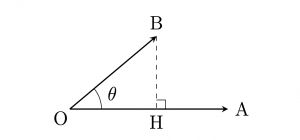
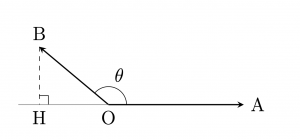
2つのベクトル\(\overrightarrow{a}=(a_1,a_2)\),
\(\overrightarrow{b}=(b_1,b_2)\)に対して,次が成り立つ.
$$\overrightarrow{a}\cdot\overrightarrow{b}=a_1b_1+a_2b_2$$
を
余弦定理
を用いて証明する.
また,ベクトルの平行・垂直と内積との関係
\(\overrightarrow{0}\)でない2つのベクトル
\(\overrightarrow{a}\)と\(\overrightarrow{b}\)
について,次が成り立つ.
- \(\overrightarrow{a}\)と\(\overrightarrow{b}\)が平行 \(\Longleftrightarrow \overrightarrow{a}\cdot\overrightarrow{b}=\pm|\overrightarrow{a}||\overrightarrow{b}|\)
- \(\overrightarrow{a}\)と\(\overrightarrow{b}\)が垂直 \(\Longleftrightarrow \overrightarrow{a}\cdot\overrightarrow{b}=0\)
- \(\overrightarrow{a}\cdot\overrightarrow{b} =\overrightarrow{b}\cdot\overrightarrow{a} \hspace{10pt}\)〔交換法則〕
- \(\overrightarrow{a}\cdot(\overrightarrow{b}\pm\overrightarrow{c}) =\overrightarrow{a}\cdot\overrightarrow{b}\pm\overrightarrow{a}\cdot\overrightarrow{c} \hspace{10pt}\)〔分配法則〕
- \((k\overrightarrow{a})\cdot\overrightarrow{b} =\overrightarrow{a}\cdot(k\overrightarrow{b}) =k(\overrightarrow{a}\cdot\overrightarrow{b}) \hspace{10pt}(k\in\mathbb{R})\)
最後にこれまでの結果をまとめておく.
$$\overrightarrow{a}\cdot\overrightarrow{b}
=|\overrightarrow{a}||\overrightarrow{b}|\cos\theta
=a_1b_1+a_2b_2
\hspace{15pt},\hspace{15pt}
\cos\theta
=\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}
=\frac{a_1b_1+a_2b_2}{\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}}$$
