命題.
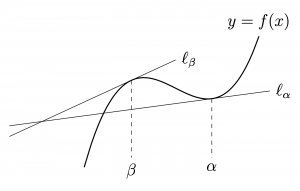
曲線\(y=f(x)\)上の異なる\(2\)点
$$
(\alpha,f(\alpha)), \
(\beta,f(\beta))
$$
における接線をそれぞれ
\(\ell_\alpha, \ell_\beta\)
とし,
この\(2\)接線が交点を持つとする.
このとき,交点の\(x\)座標は,
積分を用いて,
$$
x=\frac{\ \displaystyle\int_\alpha^\beta tf^{\prime\prime}(t)\ dt\ }
{\ \displaystyle\int_\alpha^\beta f^{\prime\prime}(t)\ dt\ }
$$
と表せる.

上の公式は,その見た目の形は複雑であるが, 計算が楽に行えるという利点がある. これは, \(2\)次導関数を用いているため,\(f(x)\)の次数が\(2\)下がることと, 定数項と\(1\)次の項を無視することができるからである.
