
これらの辺の比が等しいことから, $$\frac{\Delta s}{\Delta x}=\frac{t}{h}$$ が成り立つことに注意すると, 次の有限変換定理を得る.
$$\bigtriangleup{\rm{PP’P”}}
=\frac{1}{2}h\Delta s
=\frac{1}{2}t\Delta x
=\frac{1}{2}\mbox{□}{\rm{QQ’R’R}}
$$
\(t,y\)を\(x\)の関数とみて, \(t=t(x)\),\(y=y(x)\)(\(=f(x)\))と表す. 点\({\rm{P}}(x,y(x))\)であった. 曲線\(C\)と直線\({\rm{OP}}\)で囲まれる部分を\(\Sigma\)とする.
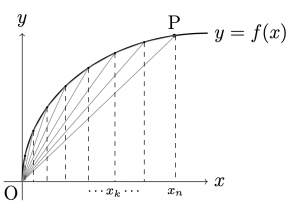
$$\Sigma
=\lim_{\Delta x\rightarrow 0}\sum_{k=0}^{n-1}\frac{1}{2}t(x_k)\Delta x
=\frac{1}{2}\int_0^x t(x) dx
$$
このように,\(\Sigma\)の求積において, \(t(x)\)が重要な役割をすることがわかる. ライプニッツは,特にこの変数\(t(x)\)を resectaと名付けた.
はじめの図において, 線分\({\rm{PQ}}\)に着目することで,
$$
t(x)=y(x)-x\frac{\Delta y}{\Delta x}
\longrightarrow
y(x)-x y'(x)
\hspace{20pt}
(\Delta x \rightarrow 0)
$$
を得る.
ここで,\(y'(x)\)は,\(y(x)\)の導関数である.
\(y'(x)\)は,点\({\rm{P}}\)における接線の傾きであるから, 上の関係式は, resecta \(t(x)\)を介して, 求積問題と接線問題をつなげる重要な関係式であると 見ることができる.
ライプニッツは,上で述べた変換定理を4分円に適用し, その面積の級数を用いた表示に成功した. 今日では,4分円の面積は\(\frac{\pi}{4}\)であることが知られているので, この級数表示は,\(\pi\)の級数表示としても有名である.
中心が\({\rm{M}}(a,0)\)で半径が\(a\)の半円\((x-a)^2+y^2=a^2\)を考える. 点\({\rm{P}}(x,y)\)とし, 点\({\rm{P}}\)を接点とする接線と \(y\)軸との交点を\({\rm{T}}(0,t)\)とする.
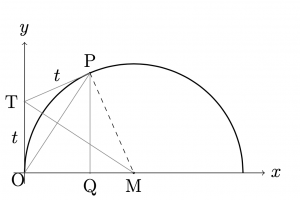
$$
\Sigma
=\frac{1}{2}\int_0^x t(x) dx
=\frac{1}{2}\left\{tx-\int_0^t x(t) dt\right\}
=\frac{1}{2}tx-a\int_0^t \frac{t^2}{a^2+t^2} dt
$$
が成り立つ.
ここで,最右辺の積分が,
$$
\displaystyle\int_0^t \frac{t^2}{a^2+t^2} dt
=\displaystyle\int_0^t \frac{\left(\frac{t}{a}\right)^2}{1+\left(\frac{t}{a}\right)^2} dt
=\displaystyle\int_0^t
\left\{
\left(\frac{t}{a}\right)^2-\left(\frac{t}{a}\right)^4+\cdots\right\} dt
=a\left\{
\frac{1}{3}\left(\frac{t}{a}\right)^3-\frac{1}{5}\left(\frac{t}{a}\right)^5+\cdots
\right\}
$$
と級数展開できることは,当時のライプニッツにおいては既知であった.
これにより, 扇型\({\rm{OMP}}\)の面積は,
$$
\Sigma+\bigtriangleup{\rm{OMP}}
=\frac{1}{2}tx-a\int_0^t \frac{t^2}{a^2+t^2} dt+\frac{1}{2}ay
=at-a^2\left\{
\frac{1}{3}\left(\frac{t}{a}\right)^3-\frac{1}{5}\left(\frac{t}{a}\right)^5+\cdots
\right\}
=a^2\left\{
\left(\frac{t}{a}\right)+
\frac{1}{3}\left(\frac{t}{a}\right)^3-\frac{1}{5}\left(\frac{t}{a}\right)^5+\cdots
\right\}
$$
と計算できる.
最後に,\(a=t=1\)とすることで, (単位円の)4分円の面積は, $$\int_0^1 y(x) dx = 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$ と求められる.
この右辺の級数は,
グレゴリー・ライプニッツ級数と呼ばれている. もし直接に左辺の積分を行おうとすると, \(\int_0^1\sqrt{x(2a-x)}dx\)という無理式の積分を扱わなければならない. これをライプニッツは変換定理により乗り越えたのである. また,(単位円の)4分円の面積は,\(\frac{\pi}{4}\)であることを用いると, 次の良く知られた\(\pi\)の級数表示が得られる. $$\frac{\pi}{4} = 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$
この記事は, [中村1980], [上垣2006] を参考にさせていただいています.
