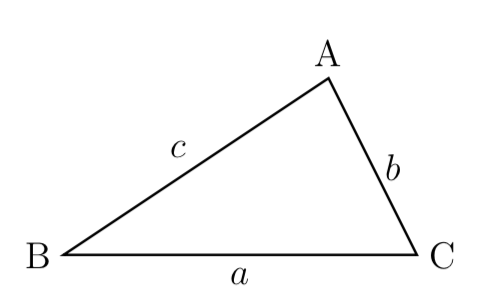
\( \bigtriangleup\rm{ABC}\) に対して, 頂点\(\rm{A},\rm{B}, \rm{C}\)の対辺の長さを それぞれ, \(a, b, c\) とし, \(\angle\rm{A},\angle\rm{B}, \angle\rm{C}\)の大きさを, それぞれ,\(A, B, C\)とする. この時,次が成り立つ.
\[a^2=b^2+c^2-2bc\cos A
\hspace{20pt},\hspace{20pt}
\cos A = \displaystyle\frac{b^2+c^2-a^2}{2bc} \]
\[b^2=c^2+a^2-2ca\cos B
\hspace{20pt},\hspace{20pt}
\cos B = \displaystyle\frac{c^2+a^2-b^2}{2ca} \]
\[c^2=a^2+b^2-2ab\cos C
\hspace{20pt},\hspace{20pt}
\cos C = \displaystyle\frac{a^2+b^2-c^2}{2ab} \]
重要な定理であるが, 三角比の定義と, 三平方の定理を用いることで簡単に証明できる.
