場合の数の基礎

高校数学By gleamath
同じ条件下で繰り返し行うことのできる実験や観察などのことを 試行といい， 試行によって，起こる結果のことを事象という． ある事象の起こり方の総数のことを場合の数 という．

ある事象の場合の数を数えるときは，

もれなく，重なりなく

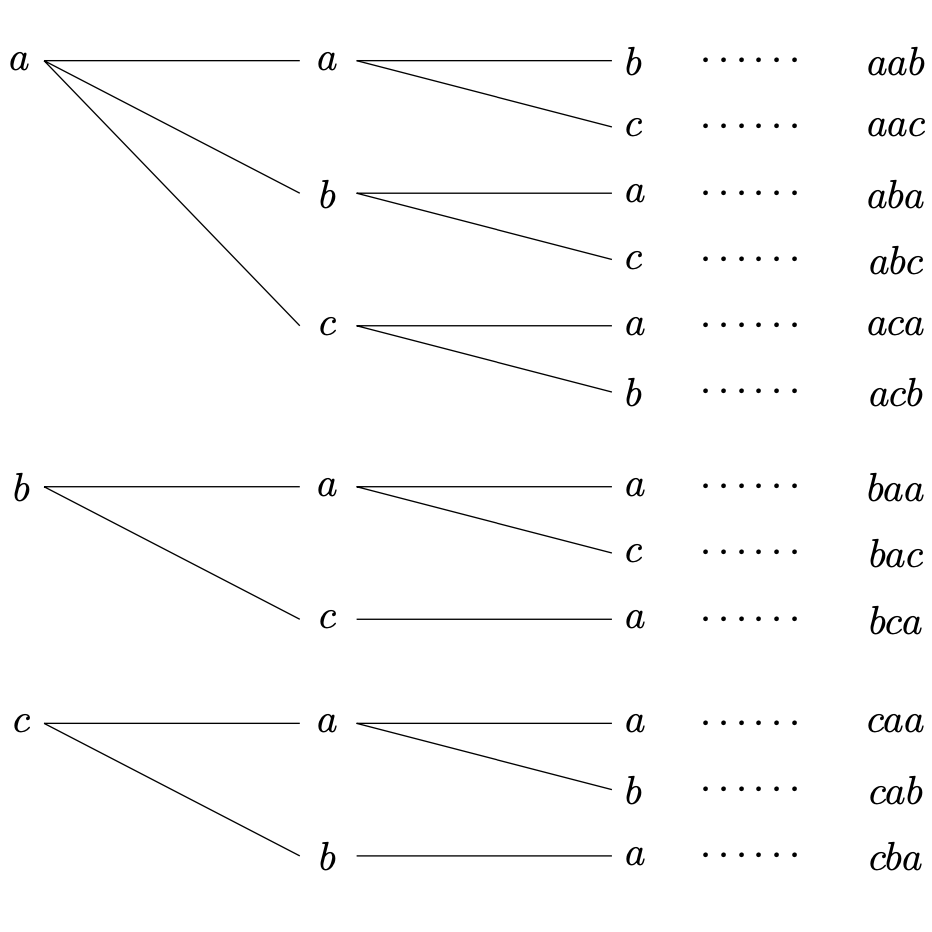
数える必要がある． そのためには，ある規則に基づいて， 順序正しく数えることが大切である． そのための方法として， 樹形図というものを使った方法を紹介する．

例．アルファベット\(a,a,b,c\)を１列に並べる場合の数を数える． ３種類の文字\(a,b,c\)に， \(a\to b\to c\)の順番で優先順位をつけて， 下のように順序正しく書き出す．
樹形図の例題を見たあと， 和の法則と積の法則と呼ばれる重要な法則について紹介し， それぞれ，簡単な例題を解説する．

和の法則

２つの事象\(A, B\)が，同時には起こらないとする． 事象\(A\)の場合の数が\(m\)通り， 事象\(B\)の場合の数が\(n\)通りとするとき， 事象\(A\)または\(B\)が起こる場合の数は， \(m+n\)通りである．


積の法則

事象\(A\)の場合の数が\(m\)通りであるとし， その各々において， 事象\(B\)の場合の数が\(n\)通りであるとする． このとき， 事象\(A\)と\(B\)がともに起こる場合の数は， \(mn\)通りである．



PDF