命題(\(\frac{1}{12}\)公式)
\(f(x)=ax^2+bx+c\)とする.
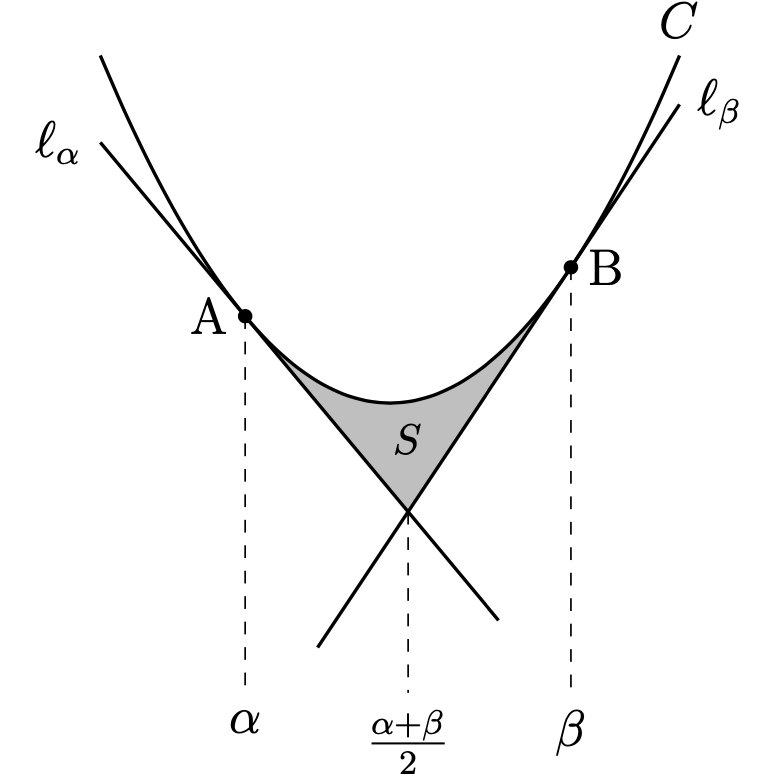
放物線\(C:y=f(x)\)上の異なる2点
\({\rm{A}}(\alpha,f(\alpha))\),\({\rm{B}}(\beta,f(\beta))\)
(ただし\(\alpha<\beta\)とする)
における接線をそれぞれ
\(\ell_\alpha,\ \ell_\beta\)とする.
このとき,
2接線\(\ell_\alpha,\ \ell_\beta\)と
放物線\(C\)で囲まれる部分の面積\(S\)について
次が成り立つ.
$$
S
\ =\
\frac{|a|}{12}(\beta-\alpha)^3
$$
図で示しているとおり, \(x\)座標において, 2接線の交点が, 2接点の真ん中に位置する という性質も重要である.
図で示しているとおり, \(x\)座標において, 2接線の交点が, 2接点の真ん中に位置する という性質も重要である.
三次曲線とその接線に関する面積公式 も\(\frac{1}{12}\)公式と呼ばれることがあるが 上の命題とは違うものなので注意すること.
