まずは,パスカルの三角形の作り方から紹介する.
- 各行の両端に「1」を記入する.
- 隣合う数字を足し合わせた数を下の行に記入する.
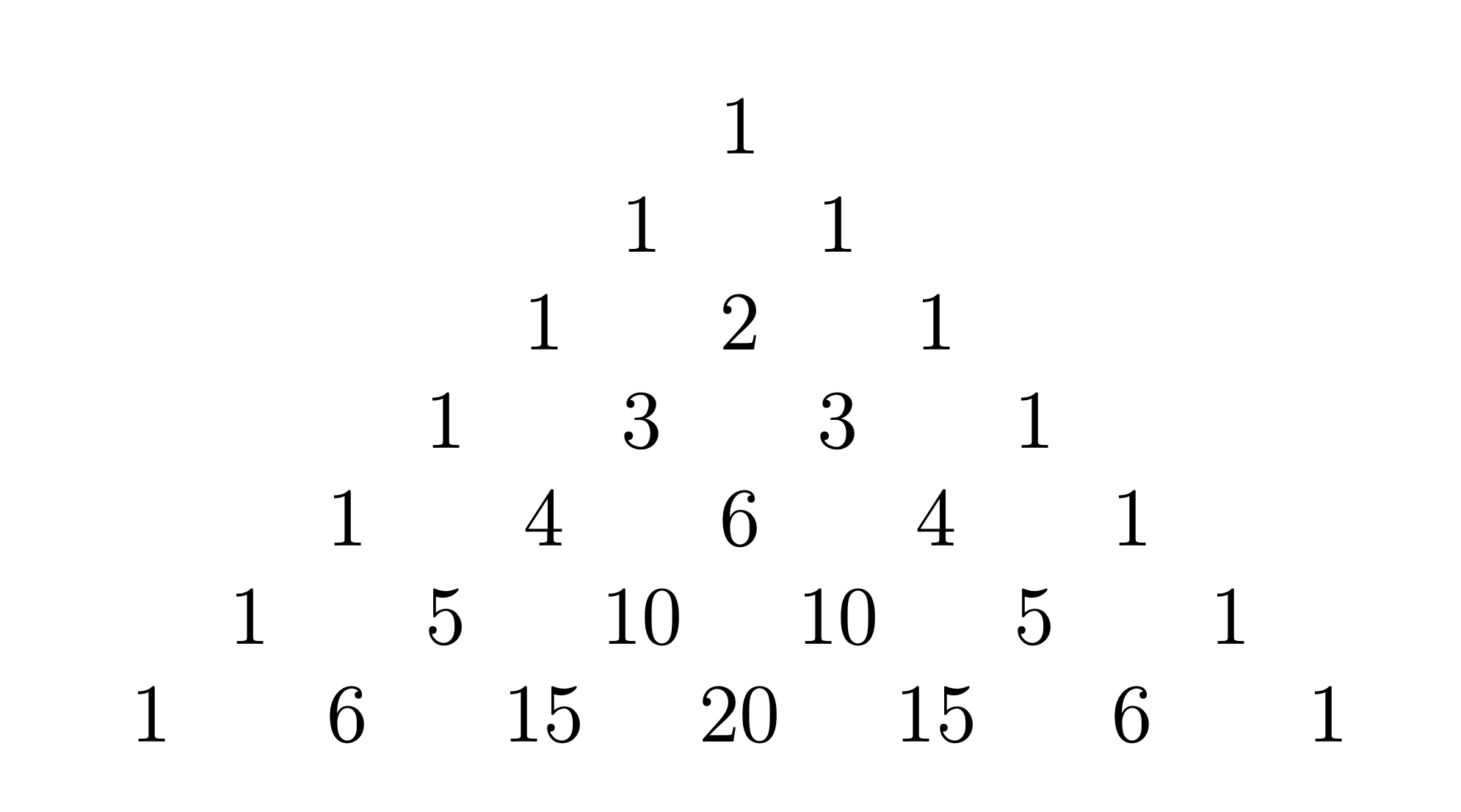
パスカルの三角形と二項係数の関係
\(n\geq0, r\geq0\)として,
パスカルの三角形における,
\(n+1\)行目の左から\(r+1\)番目の数が
$$
{_n}{\rm{C}}_r=\frac{n!}{r!(n-r)!}
$$
となっている.
パスカルの三角形の各行の和
\(n\geq0\)に対して,
パスカルの三角形における,
\(n+1\)行目の全ての数の和は,
\(2^n\)である.
よって,二項係数との関係から,次が成り立つ.
$$\sum_{r=0}^n{_n}{\rm{C}}_r=2^n.$$
