定義. 鋭角三角形\({\rm{ABC}}\)において,
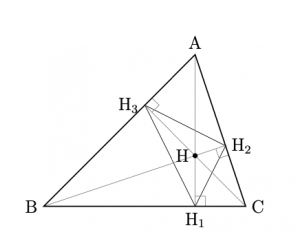
- 頂点\({\rm{A,B,C}}\)から対辺に下ろした垂線の足をそれぞれ, \({\rm{H}}_1,{\rm{H}}_2,{\rm{H}}_3\)とする. このとき,\(\bigtriangleup{\rm{H}}_1{\rm{H}}_2{\rm{H}}_3\) を\(\bigtriangleup{\rm{ABC}}\)の 垂足三角形といい, 以下では, \(\bigtriangleup\mathcal{H}\) で表す.
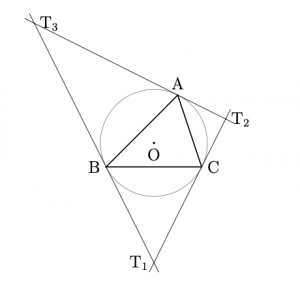
- 外接円の 頂点\({\rm{A,B,C}}\)における接線をそれぞれ \(\ell_{\rm{A}},\ell_{\rm{B}},\ell_{\rm{C}}\) とし, \(\ell_{\rm{B}}\)と\(\ell_{\rm{C}}\), \(\ell_{\rm{C}}\)と\(\ell_{\rm{A}}\), \(\ell_{\rm{A}}\)と\(\ell_{\rm{B}}\) の交点をそれぞれ, \({\rm{T}}_1,{\rm{T}}_2,{\rm{T}}_3\)とする. \(\bigtriangleup{\rm{T}}_1{\rm{T}}_2{\rm{T}}_3\) を以下では, \(\bigtriangleup\mathcal{T}\) で表す.
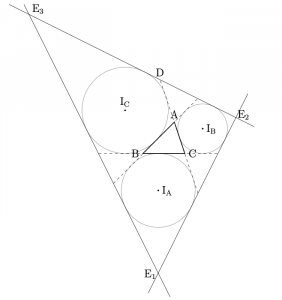
- 頂角\({\rm{A,B,C}}\)内の傍心をそれぞれ, \({\rm{I_A,I_B,I_C}}\)とし,これらを中心とする傍接円もまた同じ記号で表す. 傍接円\({\rm{I_B}}\)と\({\rm{I_C}}\), \({\rm{I_C}}\)と\({\rm{I_A}}\), \({\rm{I_A}}\)と\({\rm{I_B}}\) の外側共通接線 ( \(4\)本の共通接線のうち, \(\bigtriangleup{\rm{ABC}}\)の各辺の延長線でないもの. )をそれぞれ, \(\ell’_{\rm{A}},\ell’_{\rm{B}},\ell’_{\rm{C}}\) とし, \(\ell’_{\rm{B}}\)と\(\ell’_{\rm{C}}\), \(\ell’_{\rm{C}}\)と\(\ell’_{\rm{A}}\), \(\ell’_{\rm{A}}\)と\(\ell’_{\rm{B}}\) の交点をそれぞれ, \({\rm{E}}_1,{\rm{E}}_2,{\rm{E}}_3\)とする. \(\bigtriangleup{\rm{E}}_1{\rm{E}}_2{\rm{E}}_3\) を以下では, \(\bigtriangleup\mathcal{E}\) で表す.
命題.
\(3\)つの三角形
\(\bigtriangleup\mathcal{H}\),
\(\bigtriangleup\mathcal{T}\),
\(\bigtriangleup\mathcal{E}\)
の対応する各辺はそれぞれ平行であり,
これらの三角形は相似である.
