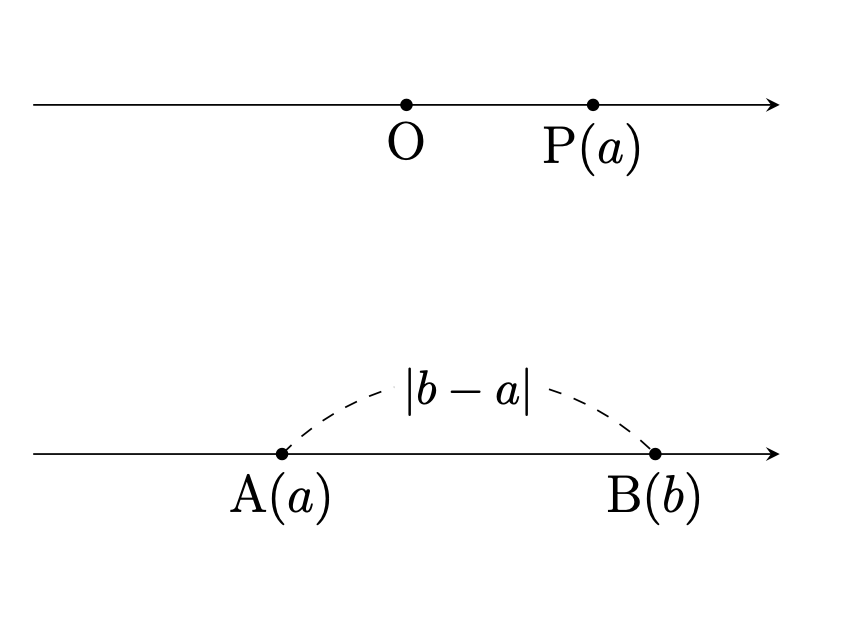
点\({\rm{P}}\)に実数\(a\)が対応するとき, \(a\)を点\({\rm{P}}\)の座標といい, \({\rm{P}}(a)\)と表す.
原点\({\rm{O}}\)と,
点\({\rm{P}}(a)\)の間の距離は,
$$
{\rm{OP}}=|a|
$$
であり,
2点\({\rm{A}}(a), {\rm{B}}(b)\)
の間の距離は,
$$
a\leq b \mbox{のとき}{\rm{AB}}=b-a
$$
$$
a> b \mbox{のとき}{\rm{AB}}=a-b
$$
なので,まとめて次のように書ける:
$${\rm{AB}}=|b-a|=|a-b|.$$
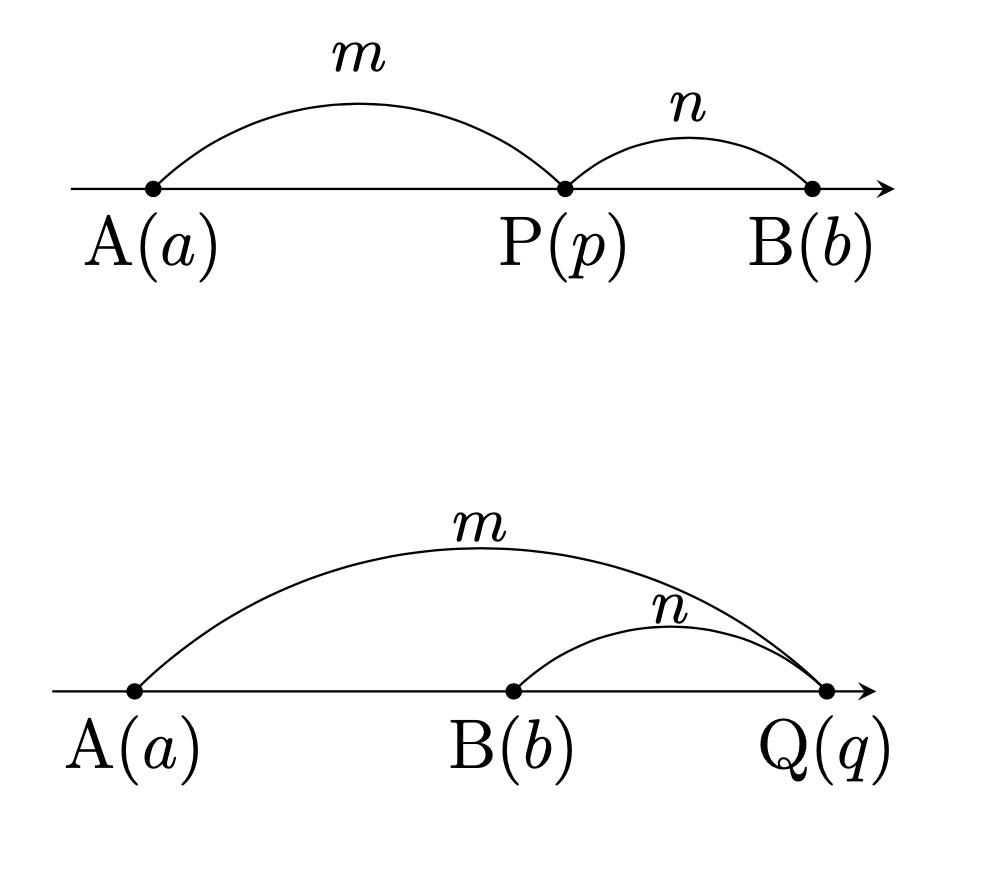
2点\({\rm{A}}(a), {\rm{B}}(b)\)に対して,
線分\({\rm{AB}}\)を\(m:n\)に内分する点\({\rm{P}}(p)\)の座標は $$p=\frac{na+mb}{m+n},$$
線分\({\rm{AB}}\)を\(m:n\)に外分する点\({\rm{Q}}(q)\)の座標は $$q=\frac{-na+mb}{m-n}$$ である.
線分\({\rm{AB}}\)を\(m:n\)に内分する点\({\rm{P}}(p)\)の座標は $$p=\frac{na+mb}{m+n},$$
線分\({\rm{AB}}\)を\(m:n\)に外分する点\({\rm{Q}}(q)\)の座標は $$q=\frac{-na+mb}{m-n}$$ である.
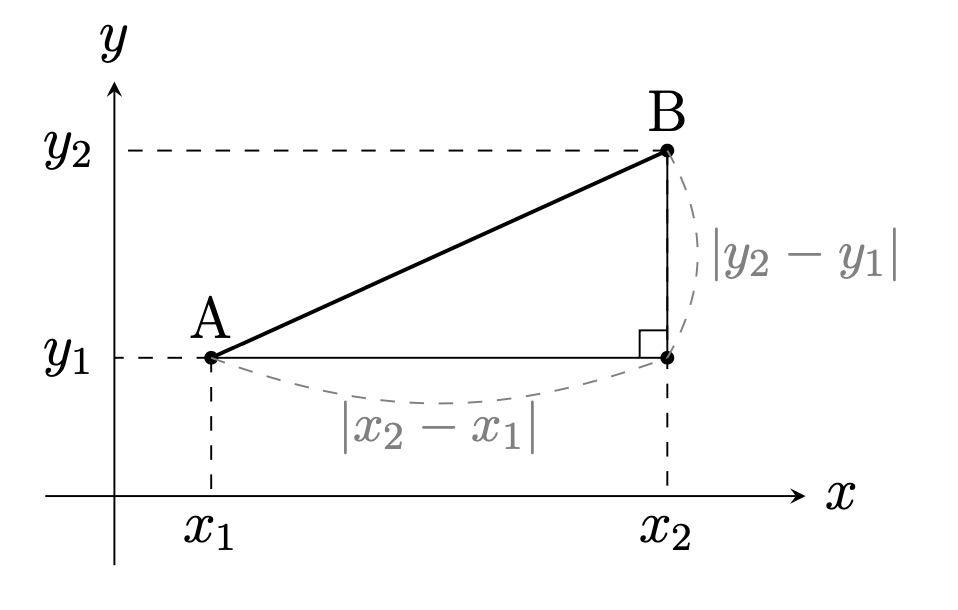
次に平面上の点について考えよう.
点\({\rm{O}}\)を原点とする座標平面上に2点 \({\rm{A}}(x_1,y_1)\),\({\rm{B}}(x_2,y_2)\) をとる.
2点\({\rm{A}}, {\rm{B}}\)の距離は,
三平方の定理から,
$${\rm{AB}}
=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
と求められる.
特に原点からの距離は,
$${\rm{OA}}
=\sqrt{x_1^2+y_1^2}
$$
と表される.
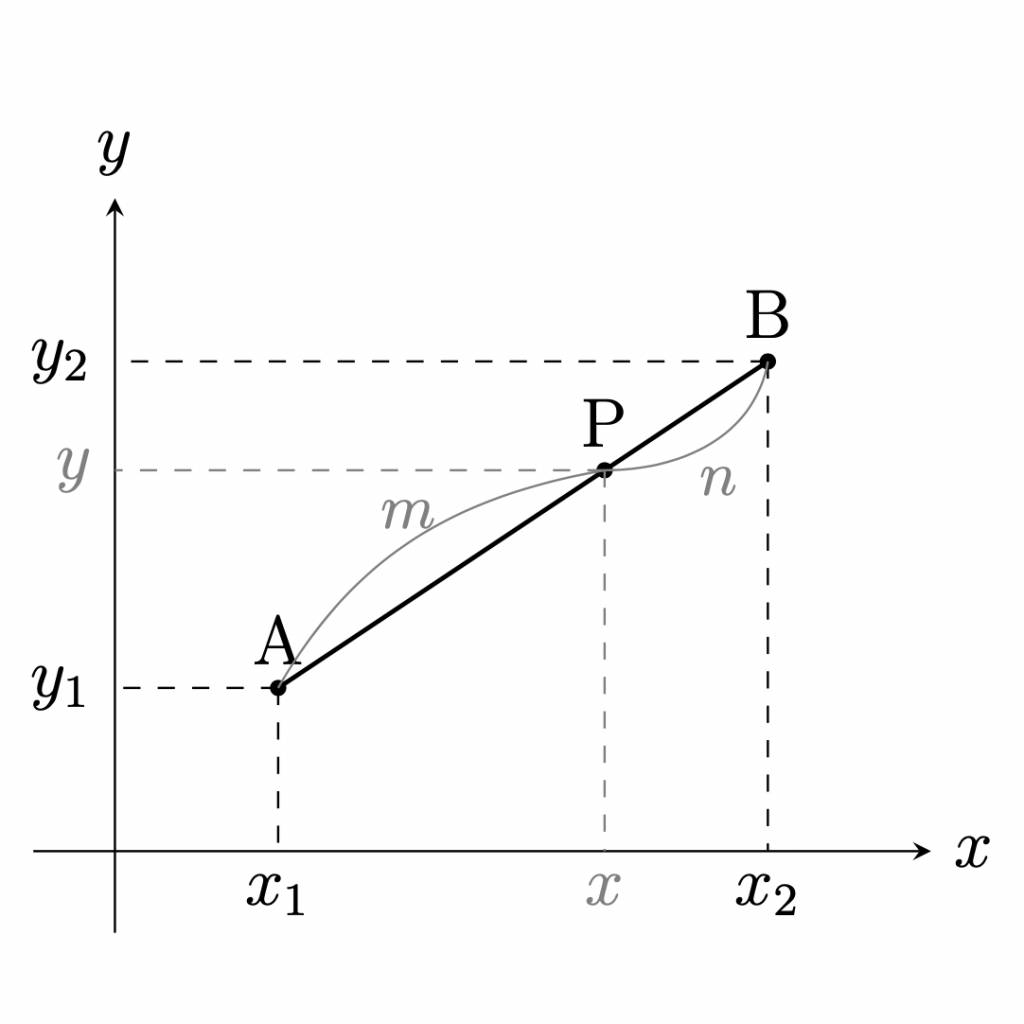
2点\({\rm{A}}(x_1,y_1)\),\({\rm{B}}(x_2,y_2)\)に対して,
線分\({\rm{AB}}\)を\(m:n\)に内分する点\({\rm{P}}\)の座標は $${\rm{P}}\left(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n}\right)$$
線分\({\rm{AB}}\)を\(m:n\)に外分する点\({\rm{Q}}\)の座標は $${\rm{Q}}\left(\frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n}\right)$$ である.
線分\({\rm{AB}}\)を\(m:n\)に内分する点\({\rm{P}}\)の座標は $${\rm{P}}\left(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n}\right)$$
線分\({\rm{AB}}\)を\(m:n\)に外分する点\({\rm{Q}}\)の座標は $${\rm{Q}}\left(\frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n}\right)$$ である.