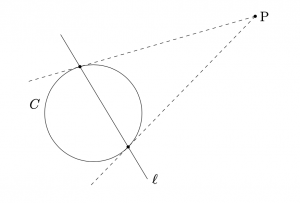
点\({\rm{P}}(p,q)\)に対する
円\(C: (x-a)^2+(y-b)^2=r^2\)の
極線の方程式は
$$
(p-a)(x-a)+(q-b)(y-b) = r^2.
$$
である.
(今,点\({\rm{P}}\)は円\(C\)の外部にあるとしているが,)
もし点\({\rm{P}}\)が,円周上にあるとすれば,
これは接線を求める方程式と同じ形をしている.
また,極線に関する下の2つの定理も証明する.
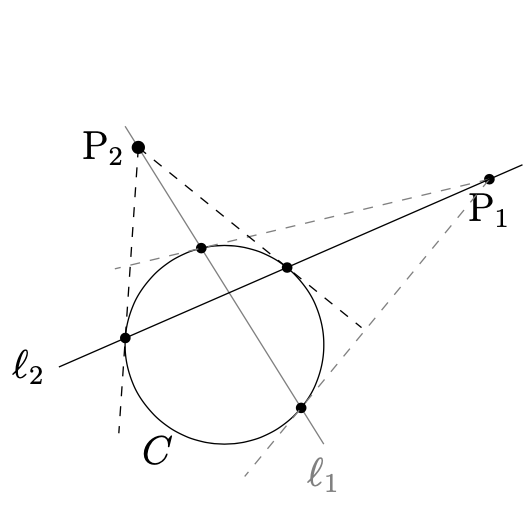
点\({\rm{P_1}}\)に対する円\(C\)の極線を\(\ell_1\)とする. このとき,
\(\ell_1\)上の任意の点\({\rm{P_2}}\)に対する 円\(C\)の極線\(\ell_2\)は,点\({\rm{P_1}}\)を通る.
ただし,2点\({\rm{P_1}}\),\({\rm{P_2}}\)は,円\(C\)の外部にあるとする.
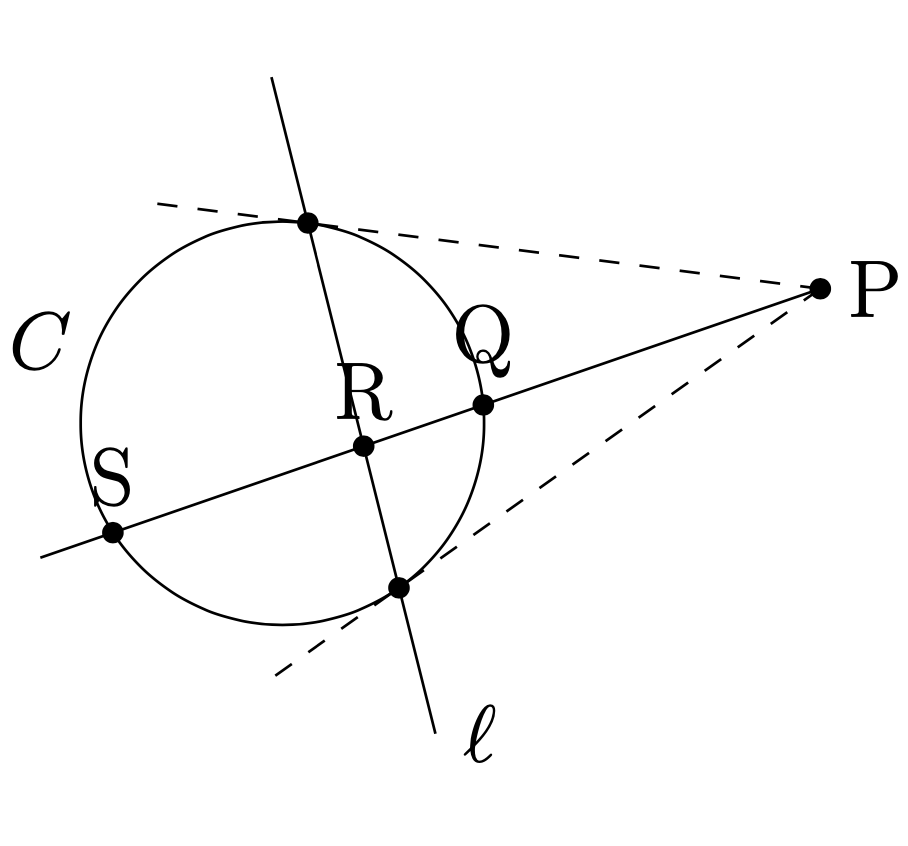
点点\({\rm{P}}\)に対する
円\(C\)の
極線を\(\ell\)とする.
右図のように,
点点\({\rm{P}}\)を通り,
円\(C\)と2点で交わる
直線を引き,
その交点をそれぞれ,
$\({\rm{Q}}\),\({\rm{S}}\)とする.
直線\({\rm{PS}}\)と極線との交点を\({\rm{R}}\)とする.
このとき,次が成り立つ.
$${\rm{PS}}\cdot{\rm{QR}}={\rm{PQ}}\cdot{\rm{RS}}$$