\(n\)を正の整数とする.
実数
\(a_i,b_i,p_i\)(\(i=1,2,\cdots,n\))に対して,
$$
\frac{a_1}{b_1}=\frac{a_2}{b_2}=\cdots=\frac{a_n}{b_n}=k
$$
が成り立つならば,
$$
\frac{p_1a_1+p_2a_2+\cdots+p_na_n}{p_1b_1+p_2b_2+\cdots+p_nb_n}=k
$$
が成り立つ.
次に加比の理の不等式版を紹介する. こちらも証明と合わせて知っておくと良い.
\(n\)を正の整数とする.
正の実数
\(a_i,b_i,p_i\)(\(i=1,2,\cdots,n\))に対して,
\begin{equation}\label{ineq}
\frac{a_1}{b_1}\leq\frac{a_2}{b_2}\leq\cdots\leq\frac{a_n}{b_n}
\end{equation}
が成り立つならば,
$$
\frac{a_1}{b_1}\leq\frac{p_1a_1+p_2a_2+\cdots+p_na_n}{p_1b_1+p_2b_2+\cdots+p_nb_n}\leq\frac{a_n}{b_n}
$$
が成り立つ.
等号が成立するのは,
仮定の不等式の等号がすべて成り立つときである.
最後に,加比の理とその不等式版の図形的な解釈を紹介する. これを知っていれば,これらの定理が当たり前であることがわかるだろう.
$$
\frac{a}{b}
\hspace{10pt}\longleftrightarrow\hspace{10pt}
y=\frac{a}{b}x
\mbox{のグラフの傾き}
\hspace{10pt}\longleftrightarrow\hspace{10pt}
\mbox{2点}
(0,0), (b,a)
\mbox{を通る直線の傾き}
$$
という対応を考えることで,
条件式を図形的に捉えることができる.
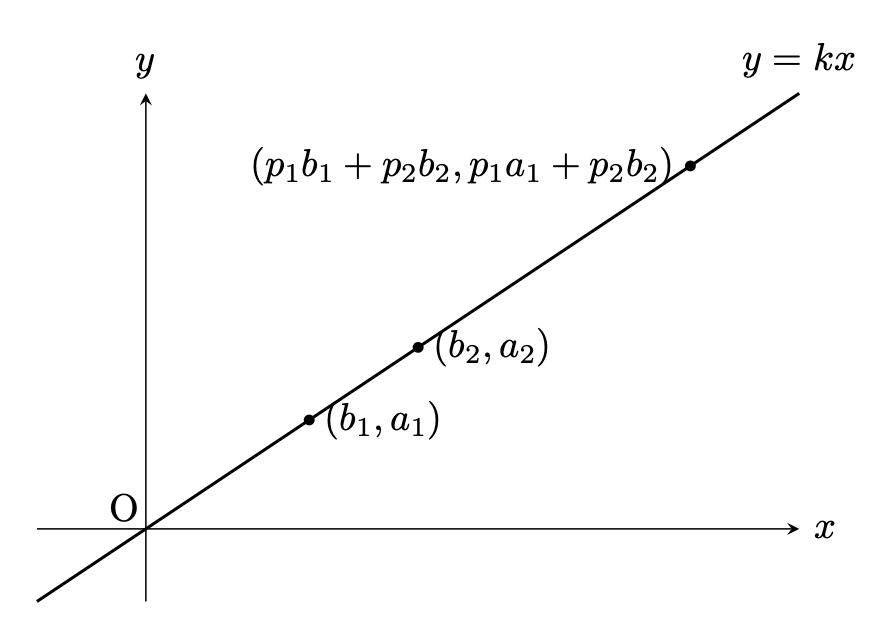
\(\displaystyle\frac{a_1}{b_1}=\frac{a_2}{b_2}=k\)は, 3点\((0,0), (b_1,a_1), (b_2,a_2)\)が, 同一直線(\(y=kx\))上にあるということであり, このとき, 点 \((p_1b_1+p_2b_2,p_1a_1+p_2b_2)\)も 同じ直線上にあることがわかる.
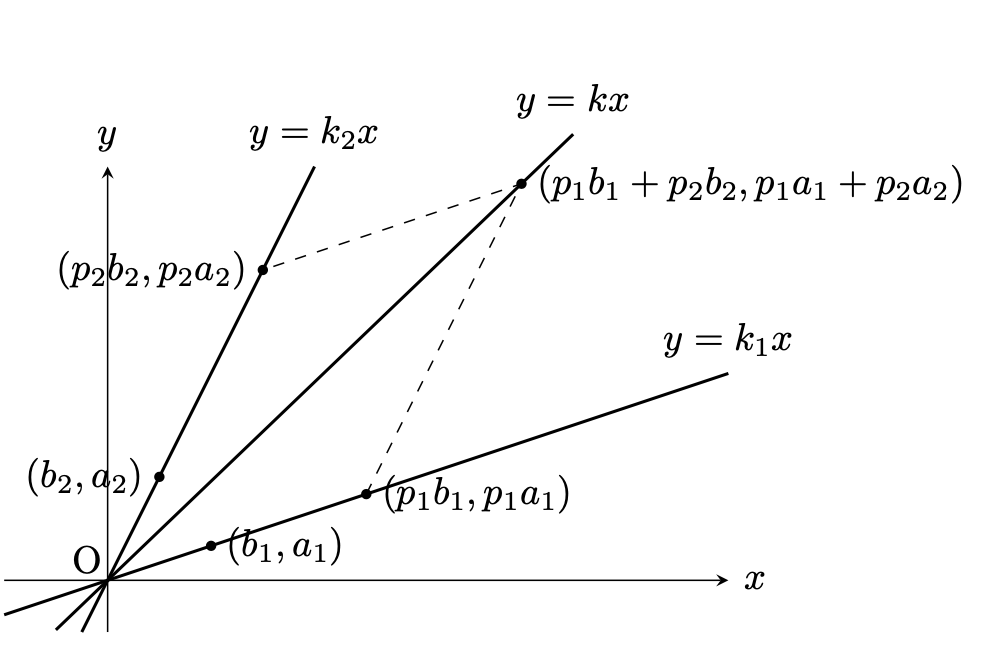
\(k_1=\displaystyle\frac{a_1}{b_1} < \frac{a_2}{b_2}=k_2\), \(\displaystyle\frac{p_1a_1+p_2a_2}{p_1b_1+p_2b_2}=k\)とすると, 直線\(y=kx\)は,下図のような平行四辺形の対角線である. 直線の傾きを比較すると, \( k_1 < k < k_2 \)が従う.