円と直線の関係

点\({\rm{C}}(a,b)\)を中心とする半径\(r\)の円 $$C : (x-a)^2+(y-b)^2=r^2$$ と， 直線 $$\ell : sx+ty+u=0$$ の位置関係は，次の３つに分類される．

• 異なる２点で交わる．
• １点で接する．
• 共有点を持たない．

それぞれの方程式から， 位置関係を判断する方法を考えよう．

1. 中心と直線の距離\(d\)と半径\(r\)による分類方法

まずは， 点と直線の距離 の公式を思い出す． 円\(C\)の中心\({\rm{C}}(a,b)\)と， 直線\(\ell\)の距離を\(d\)とすると $$ d=\frac{\mid sa+tb+u \mid}{\sqrt{s^2+t^2}} $$ と書けるのであった． この\(d\)と， 円の半径\(r\)との大小関係から，円と直線の関係を分類できる． すなわち，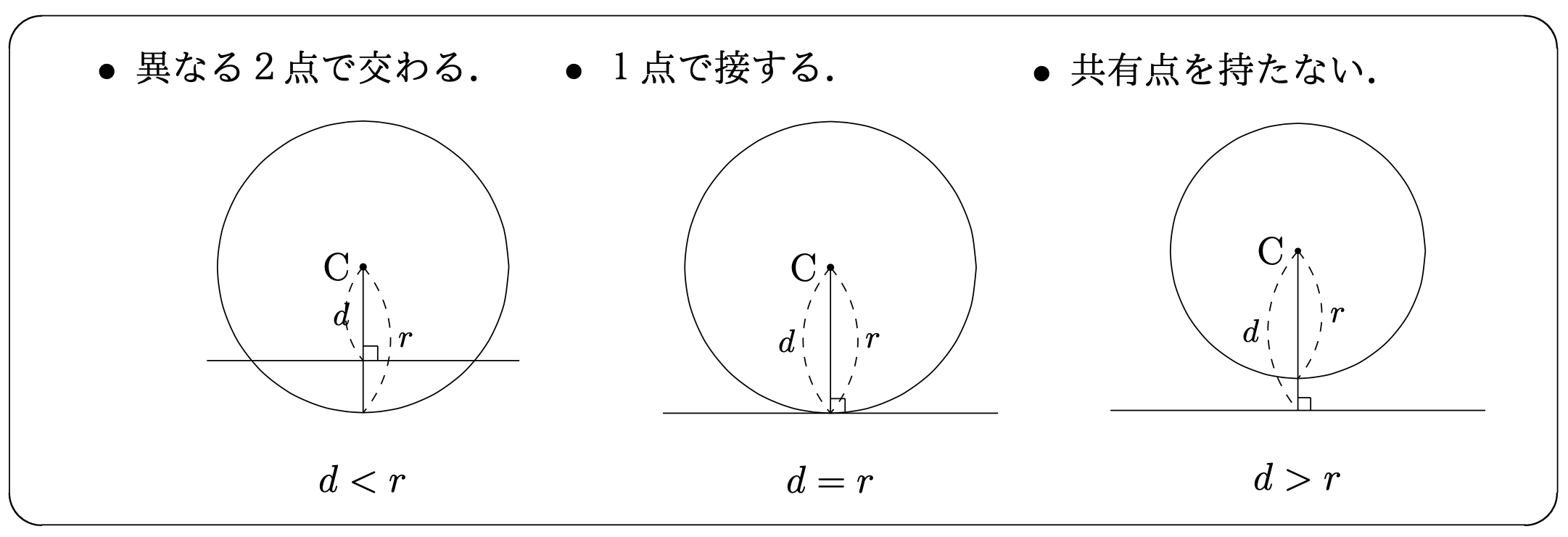

と分類できる．

2. 連立方程式の実数解の個数による分類方法

円の方程式と直線の方程式による連立方程式を考える． $$ \left\{ \begin{array}{lll} (x-a)^2+(y-b)^2=r^2&&\\ sx+ty+u=0&& \end{array} \right. $$ この連立方程式の実数解は，円と直線の共有点に対応しているので， その個数から位置関係を分類できる． 必要なのは実数解の個数だけなので， 判別式を用いれば十分である． 上の連立方程式において， \(y\)または\(x\)を消去して得られる \(x\)または\(y\)の２次方程式の判別式を \(D\)とする．このとき 判別式の符号と実数解の個数の関係から， 次のように分類できる．

最後に直線と円が異なる２点で交わる場合， その２つの共有点を通る円について考察する． 通る２点の情報だけでは，円は１つに決まらないが， 変数\(k\)を用いて，これらの円たちを統一して記述することができる． この証明の理解には， 円の方程式 の基本形と一般形の関係を理解していることが 必要である．


PDF