集合と要素と部分集合

範囲がはっきりしたものの集まりを集合といい， 集合を構成している１つ１つのものを、その集合の 要素または元という．

集合と要素について， はじめは下図のようなイメージを持つと良い． 下図は， 集合\(A\)において，

\(a,b\)は\(A\)の要素であるが， \(c\)は\(A\)の要素ではない．

ということを表している． このことを

$$a\in A,\hspace{3pt} b\in A,\hspace{3pt} c\not\in A$$

と表す．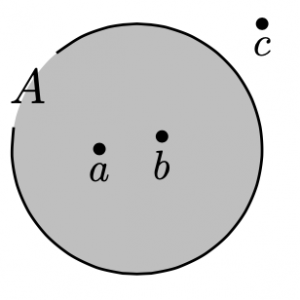

次に，集合の表し方を定義する．
以下はどちらも「一桁の奇数」の集合を表す． 要素を１つも持たない集合のことを 空集合といい， \(\emptyset\)と表す．

次に部分集合や集合が等しいということを定義する．

２つの集合\(A,B\)において， 「\(x\in A\Rightarrow x\in B\)」が成り立つとき， \(A\)は\(B\)の部分集合， といい， $$A\subset B$$ と表す．

「\(A\subset B\)かつ\(B\subset A\)」が成り立つとき， \(A\)と\(B\)は等しいといい， $$A =B$$と表す．

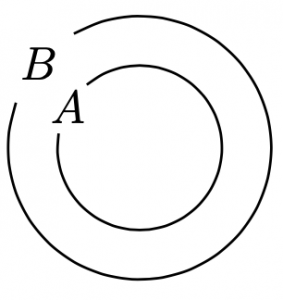
空集合\(\emptyset\)は，全ての集合の部分集合を定義する．

記号\(<\)と，記号\(\subset\)を混同してはならない． 部分集合の定義から， 任意の集合\(A\)に対して，\(A\subset A\) （\(A\)は\(A\)自身の部分集合である）が成り立つ． また上では，集合\(A,B\)に対して， \(A=B\)であることを「\(A\subset B\)かつ\(B\subset A\)」 が成り立つことと定義したが， これは， 「\(x\in A\Rightarrow x\in B\)かつ，\(x\in B\Rightarrow x\in A\)」 が成り立つということであり， すなわち， \(A\)と\(B\)の要素が一致している状態を表している


PDF