命題.
\(f(x)=ax^3+bx^2+cx+d\ (a\ne0)\)とする.
このとき,次が成り立つ.
\(\bullet\) 曲線\(C:y=f(x)\)は, 変曲点\({\rm{P}}\left(-\frac{b}{3a},f(-\frac{b}{3a})\right)\)に関して対象である.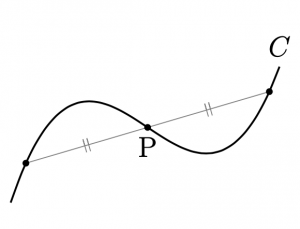
\(\bullet\) 曲線\(C:y=f(x)\)は, 変曲点\({\rm{P}}\left(-\frac{b}{3a},f(-\frac{b}{3a})\right)\)に関して対象である.


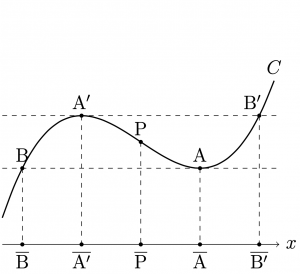
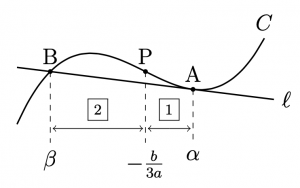
さらに,3次関数が極値を持つとし, 上の命題の極点における接線を考えることにより, 下図のように,極点,変曲点,極点における接線の交点を \(x\)軸上に射影した点は等間隔に並んでいることを証明する.