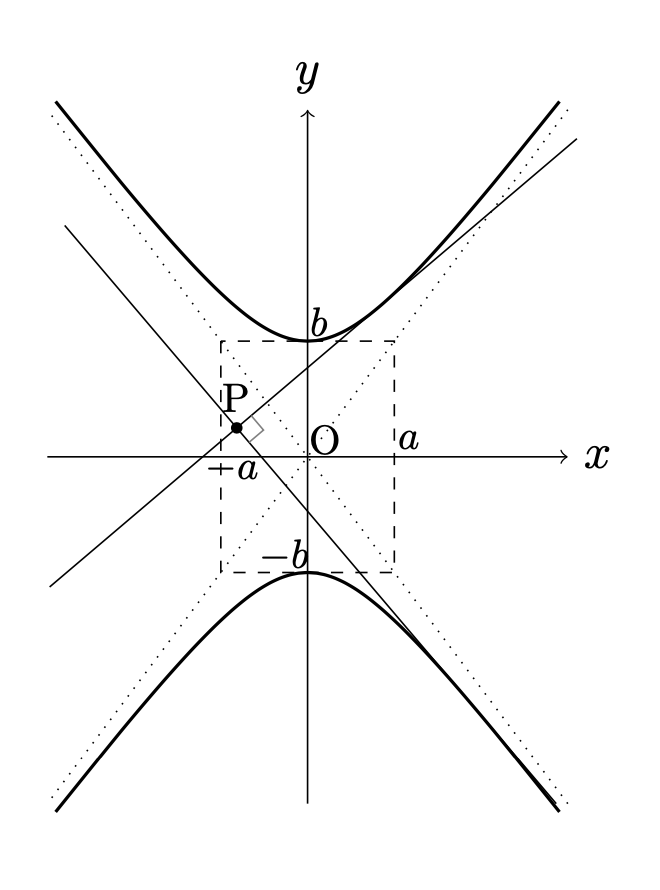
命題.
双曲線
$$H:\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$
において,
\(H\)の外側にある点\({\rm{P}}(p,q)\)を通り\(H\)に接する\(2\)本の直線が
(引けるときこの直線が)
直交する条件は,
$$
a^2-b^2=p^2+q^2
,\hspace{15pt} q\ne\pm\frac{b}{a}p
$$
が成り立つことである.
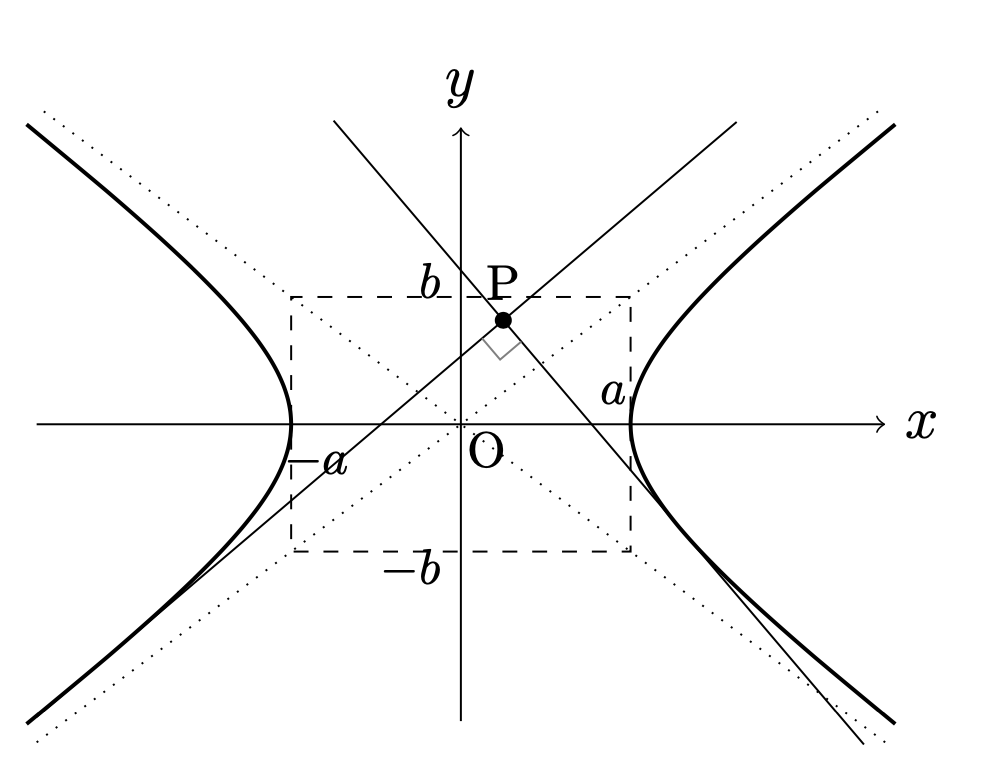
命題.
双曲線
$$H’:\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$$において,
\(H’\)の外側にある点\({\rm{P}}(p,q)\)を通り\(H’\)に接する\(2\)本の直線が
(引けるときこの直線が)
直交する条件は,
$$
-a^2+b^2=p^2+q^2
,\hspace{15pt} q\ne\pm\frac{b}{a}p
$$
が成り立つことである.