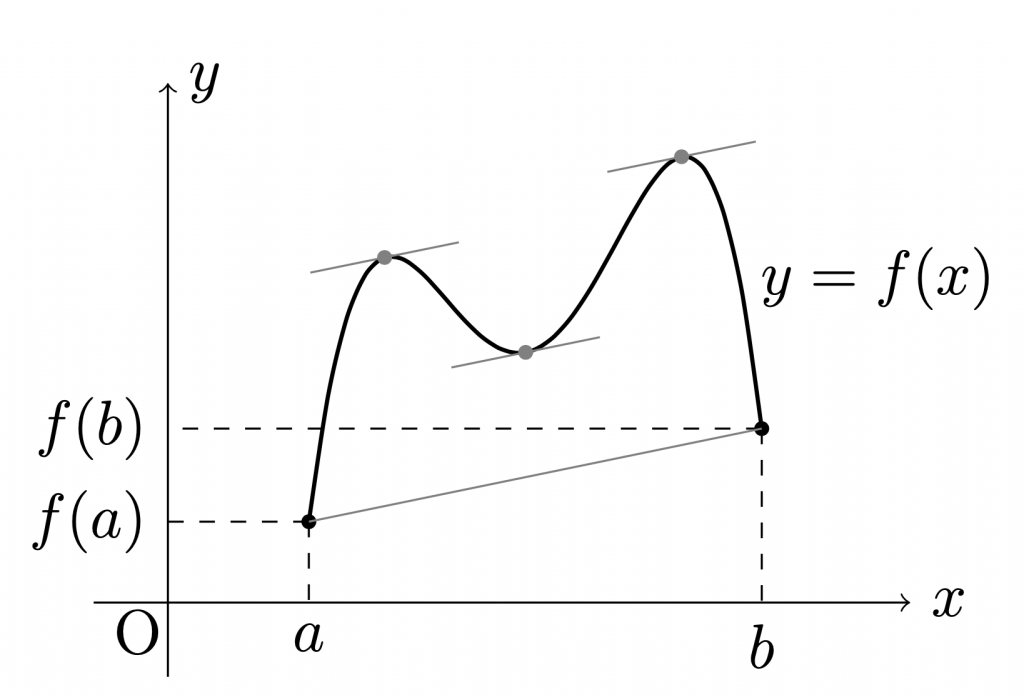
平均値の定理.
関数\(f(x)\)は,
閉区間\([a,b]\)で連続であり,
開区間\((a,b)\)で微分可能であるとする.
このとき,
$$
f'(c)=\frac{f(b)-f(a)}{b-a},
\hspace{10pt}
a < c < b
$$
を満たす実数\(c\)が存在する.
系.
\(h > 0\)とする.
関数\(f(x)\)は,
閉区間\([a,a+h]\)で連続であり,
開区間\((a,a+h)\)で微分可能であるとする.
このとき,
$$
f(a+h)=f(a)+hf'(a+h\theta),
\hspace{10pt}
0 < \theta < 1
$$
を満たす実数\(\theta\)が存在する.
