三角関数 – gleamath.com

座標平面上の原点 $\rm{O}$ を中心とする半径$r$の円を考える． $x$軸の正の部分を始線にとり，一般角$\theta$の動径と，この円との交点を${\rm{P}}(x,y)$とする．

まず，次の補題を証明する．

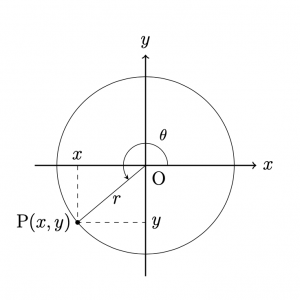
$\displaystyle\frac{y}{r}$， $\displaystyle\frac{x}{r}$， $\displaystyle\frac{y}{x}$の各値は，$r$によらず，$\theta$だけによって決まる．

これにより，上の３つの値は，$\theta$の関数と見ることができる．よって，三角関数を次のように定義することができる．

上の状況において，

$$\sin\theta = \frac{y}{r} \hspace{5pt},\hspace{5pt} \cos\theta = \frac{x}{r} \hspace{5pt},\hspace{5pt} \tan\theta = \frac{y}{x} $$

と定義し，それぞれ一般角$\theta$の 正弦（sine・サイン），余弦（cosine・コサイン），正接（tangent・タンジェント） といい，これらをまとめて三角関数という．ただし，任意の整数$n$に対して， $\theta=\displaystyle\frac{\pi}{2}+n\pi$のとき， $\tan\theta$は定義されない．

定義のように，半径$r$の円で考えるのではなく，単位円上（すなわち$r=1$）で考えることにより，

$\sin\theta, \cos\theta, \tan\theta$ はそれぞれ，点${\rm{P}}$の $y$座標，$x$座標，直線${\rm{OP}}$の傾き

と見ることができる．
また，三角関数の相互関係

$\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}$

$\sin^2\theta+\cos^2\theta=1$

$1+\tan^2\theta=\displaystyle\frac{1}{\cos^2\theta}$

や，様々な角の三角比の間の関係についても紹介する．

$\sin(2n\pi\pm\theta)=\pm\sin\theta$

$\sin(\pi\pm\theta)=\mp\sin\theta$

$\sin\left(\displaystyle\frac{\pi}{2}\pm\theta\right)=\cos\theta$

$\cos(2n\pi\pm\theta)=\cos\theta$

$\cos(\pi\pm\theta)=-\cos\theta$

$\cos\left(\displaystyle\frac{\pi}{2}\pm\theta\right)=\mp\sin\theta$

$\tan(2n\pi\pm\theta)=\pm\tan\theta$

$\tan(\pi\pm\theta)=\pm\tan\theta$

$\tan\left(\displaystyle\frac{\pi}{2}\pm\theta\right) =\mp\displaystyle\frac{1}{\tan\theta}$

PDF