まずは,標準基底を持つ自由加群を構成する. \(A\)を可換環とし, \(X\)を集合とする. 写像 \(s\in{\rm{Map}}(X,A)\)に対して, 集\(s^{-1}(0)\subset X\)の \(X\)に関する補集合を \(V_s:=X\setminus s^{-1}(0)\)で表す. \(A^{(X)}\)を \({\rm{Map}}(X,A)\) の部分集合として, $$ A^{(X)}:=\{ s\in{\rm{Map}}(X,A)\mid \#(V_s)<\infty \} $$ で定める. ここで, \(\#(V_s)<\infty\)は, 集合\(V_s\)が有限集合であることを表す. 任意の\(x\in X\)に対して,写像 \(e_x:X\to A\)を $$ e_x(y)=\left\{ \begin{array}{ccc} 1&&(y= x)\\ 0&&(y\ne x) \end{array} \right. $$ で定めると, \(V_{e_x}=X\setminus e_x^{-1}(0)=\{x\}\) は有限集合なので, \(e_x\in A^{(X)}\)である. \(A^{(X)}\)は, $$ B:=\{e_x\mid x\in X\} $$ を基底に持つ自由\(A\)加群である.
写像\(i_X\)を
$$
i_X:X\to A^{(X)}
\hspace{10pt};\hspace{10pt}
x\mapsto e_x
$$
で定め,
これを
標準写像と呼ぶ.
\(i_X\)を普遍元として,
自由\(A\)加群\(A^{(X)}\)は,
合成関手\(h^X\circ U\)を表現する.
定理.
\(h^{A^{(X)}}:{\bf{A\mbox{-}Mod}}\to{\bf{Set}}\)
を\(A\)加群\(A^{(X)}\)が表現する関手とする.
このとき,
関手の同型
$$
i_X^*:h^{A^{(X)}}\to h^X\circ U
$$
が存在する.
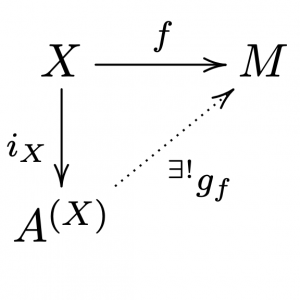
この記事は, [斎藤2020] を参考にさせていただいています.
