剰余環の普遍性

$\bf{Ring}$を（単位元を持つ可換）環の圏とする． $\bf{Ring}$の対象$A, B$に対して， $A$から$B$への射$A\to B$全体の集合を ${\rm{Mor}}(A,B)$で表す．集合全体のなす圏を$\bf{Set}$で表す． $A$を環， $I$を$A$のイデアルとする． $A$が表現する関手 $h^A:{\bf{Ring}}\to{\bf{Set}}$の部分関手 $F$を，環$B$に対して， $$ F(B) =\{f\in{\rm{Mor}}(A,B)\mid I\subset{\rm{Ker}} f\} $$ で定める．

$I$による$A$の剰余環を$A/I$で表し， $p:A\to A/I$を標準全射とする． $p$の引き戻しは，関手の同型を誘導する．

定理． 上の記号をそのまま用いる．関手の同型 $$ p^*:h^{A/I}\to F $$ が存在する．

定義.
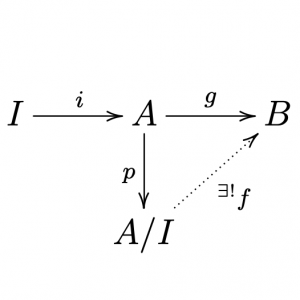
定理の関手の同型$p^*$が存在することを剰余環の普遍性 という．

定義.
$C$を圏とし， $F:C\to{\bf{Set}}$を関手とする． $C$の対象$X$と関手の同型 $h^X\to F$が存在するとき， $F$は$X$で表現される（表現可能である） という．また，この同型により， $1_X\in h^X(X)$に対応する $F(X)$の元を， $F$の普遍元という．

注意.
剰余環の普遍性とは， 剰余環$A/I$が関手$F$を表現することと言っても同じことである．普遍元は，標準全射 $p\in{\rm{Mor}}(A,A/I)$である．

定理の証明はこちら
PDF

この記事は， [斎藤2020] を参考にさせていただいています．