ここでは,ベクトルを用いて加重重心を考察する. 以下の仮定の点\({\rm{P}}\)が加重重心である.
仮定. \(a,b,c>0\)とする. \(\bigtriangleup\rm{ABC}\)の内部の点\(\rm{P}\)が $$ a\overrightarrow{\rm{PA}} +b\overrightarrow{\rm{PB}} +c\overrightarrow{\rm{PC}} =\overrightarrow{0} $$ を満たしていると仮定する.
まずは, 感覚的に加重重心が捉えやすいであろう結果を紹介する.
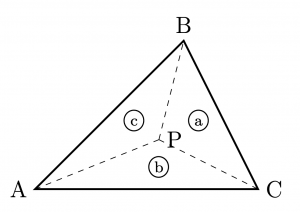
仮定の状況において, \(\bigtriangleup\rm{PBC},\bigtriangleup\rm{PCA},\bigtriangleup\rm{PAB}\) の面積比は, \(a:b:c\)である.
次に辺の比や加重重心の座標に関する2つの結果を紹介する.
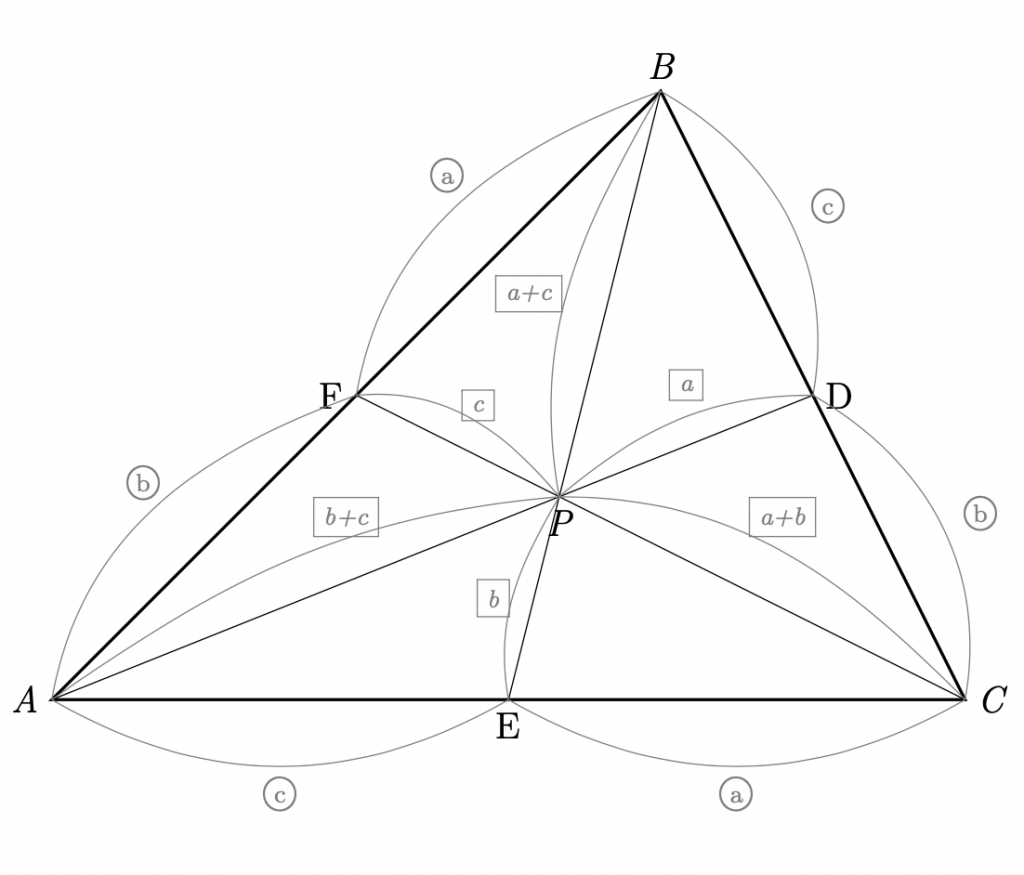
仮定の状況において, それぞれの線分の内分点に対して, 下図のように比が定まる.
注意.
たくさんの線分の比をいつの図にまとめたので,
ややこしくなってしまったが,
例えば,
図の通り,
\({\rm{AF}}:{\rm{FB}}\)
は,
\(b:a\)
であるが,
\({\rm{EC}}:{\rm{CD}}\)
は,
\(a:b\)
ではない.
上で「線分の内分点」と付け加えたのは,このような意味である.
仮定の状況において, 3点\({\rm{A,B,C}}\)の座標をそれぞれ, \((a_1,a_2), (b_1,b_2), (c_1,c_2)\)とする. このとき, 点\({\rm{P}}\)の座標は, $$\left( \displaystyle\frac{aa_1+bb_1+cc_1}{a+b+c}, \displaystyle\frac{aa_2+bb_2+cc_2}{a+b+c} \right)$$ である.
