3次関数と接線で囲まれる部分の面積

３次関数と，その接線で囲まれる部分の面積について，３次関数の対称性と，よく知られた 1/12面積公式を合わせることで，次が成り立つ．

命題．

$f(x)=ax^3+bx^2+cx+d,\ (a\ne0)$ とし，曲線

$C:y=f(x)$ 上の点

${\rm{A}}(\alpha,f(\alpha))$ における接線を

$\ell$ とする．このとき，

$C$ と

$\ell$ で囲まれる部分の面積

$S$ について，次が成り立つ．

$S =\frac{|a|}{12}\left(3\alpha+\frac{b}{a}\right)^4$ とくに，

$a=1$ ，

$b=0$ なら，次が成り立つ．

$S =\frac{27}{4}\alpha^4$

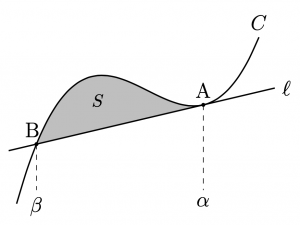
このタイプの問題は良く出題されるが，接点とは異なる交点を求めて，

$\frac{1}{12}$ 面積公式を用いるのが一般的であると思う．上の公式は，その交点すら求める必要がないことを示している．
とくに，

$x^3$ の係数が

$1$ である場合や，

$x^2$ の係数が

$0$ である場合（これは変曲点の

$x$ 座標が

$0$ である場合）など特別な場合には，さらに公式が簡単になる．

PDF