定理.
\(\alpha, \beta, \gamma>0\)とする.
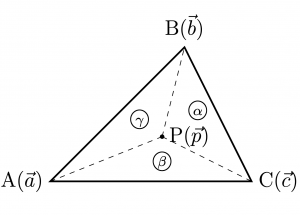
\(\bigtriangleup\rm{ABC}\)とその内部の点\({\rm{P}}\)に対して,
次の\(3\)条件は同値である:
- \(\vec{p}=\displaystyle\frac{\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}}{\alpha+\beta+\gamma},\)
- \(\alpha\overrightarrow{\rm{PA}} +\beta\overrightarrow{\rm{PB}} +\gamma\overrightarrow{\rm{PC}} =\overrightarrow{0},\)
- \(\bigtriangleup\rm{BPC}:\bigtriangleup\rm{CPA}:\bigtriangleup\rm{APB} =\alpha:\beta:\gamma.\)
\(\alpha, \beta, \gamma>0\)とする.
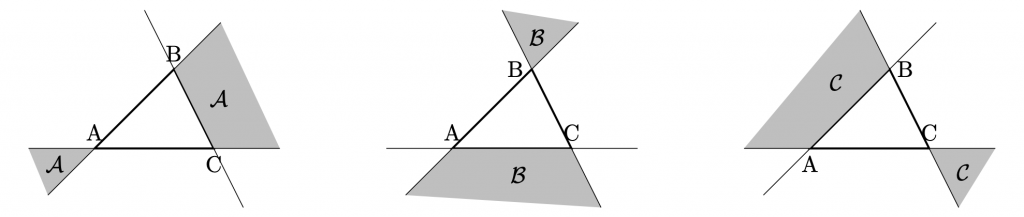
\(\bigtriangleup\rm{ABC}\)とその外部(各辺の延長線を含まない)の点\({\rm{P}}\)に対して,条件
$$\bigtriangleup\rm{BPC}:\bigtriangleup\rm{CPA}:\bigtriangleup\rm{APB}
=\alpha:\beta:\gamma$$
と,
次の条件は同値である:
-
\(\bullet\ \)点\({\rm{P}}\)が領域\(\mathcal{A}\)上にあるとき; \(\vec{p}=\displaystyle\frac{-\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}}{-\alpha+\beta+\gamma}, \hspace{20pt} -\alpha\overrightarrow{\rm{PA}} +\beta\overrightarrow{\rm{PB}} +\gamma\overrightarrow{\rm{PC}} =\overrightarrow{0}.\)
- \(\bullet\ \)点\({\rm{P}}\)が領域\(\mathcal{B}\)上にあるとき; \(\vec{p}=\displaystyle\frac{\alpha\vec{a}-\beta\vec{b}+\gamma\vec{c}}{\alpha-\beta+\gamma}, \hspace{20pt} \alpha\overrightarrow{\rm{PA}} -\beta\overrightarrow{\rm{PB}} +\gamma\overrightarrow{\rm{PC}} =\overrightarrow{0}.\)
- \(\bullet\ \)点\({\rm{P}}\)が領域\(\mathcal{C}\)上にあるとき; \(\vec{p}=\displaystyle\frac{\alpha\vec{a}+\beta\vec{b}-\gamma\vec{c}}{\alpha+\beta-\gamma}, \hspace{20pt} \alpha\overrightarrow{\rm{PA}} +\beta\overrightarrow{\rm{PB}} -\gamma\overrightarrow{\rm{PC}} =\overrightarrow{0}.\)
