接弦定理
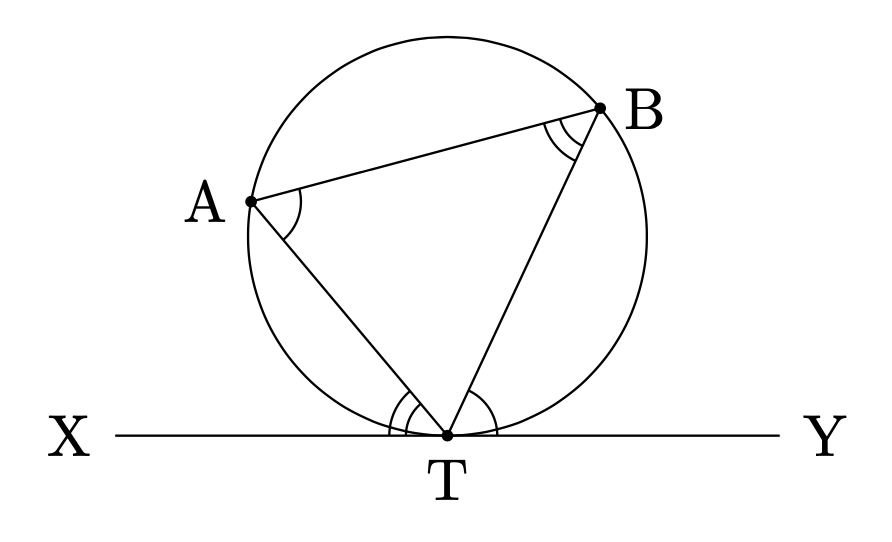
直線\( {\rm{XY}}\)が、 点\({\rm{T}}\)で円と接しているとする. 2点\({\rm{A}}\),\({\rm{B}}\)を 円周上の点とすると,次が成り立つ. $$\angle{\rm{BTY}}=\angle{\rm{TAB}}$$ $$\angle{\rm{ATX}}=\angle{\rm{TBA}}$$
接弦定理の逆
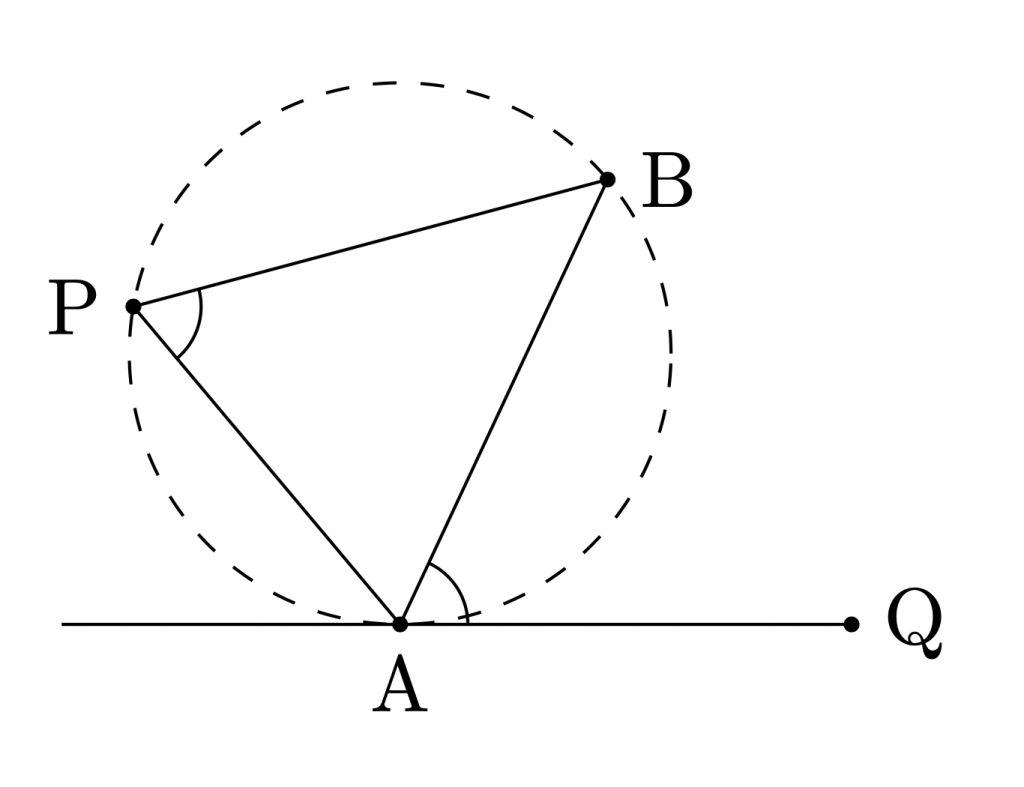
直線\({\rm{AB}}\)に対して,
点\({\rm{P}}\)と点
\({\rm{Q}}\)が反対側にあるとする.
この時,
\(\angle{\rm{BAQ}}=\angle{\rm{APB}}\)
が成り立つならば,
直線\({\rm{AQ}}\)は,
\(\bigtriangleup{\rm{APB}}\)の外接円と接する.
「円の接線は,円の中心と接点を結ぶ線分に対して垂直である」
