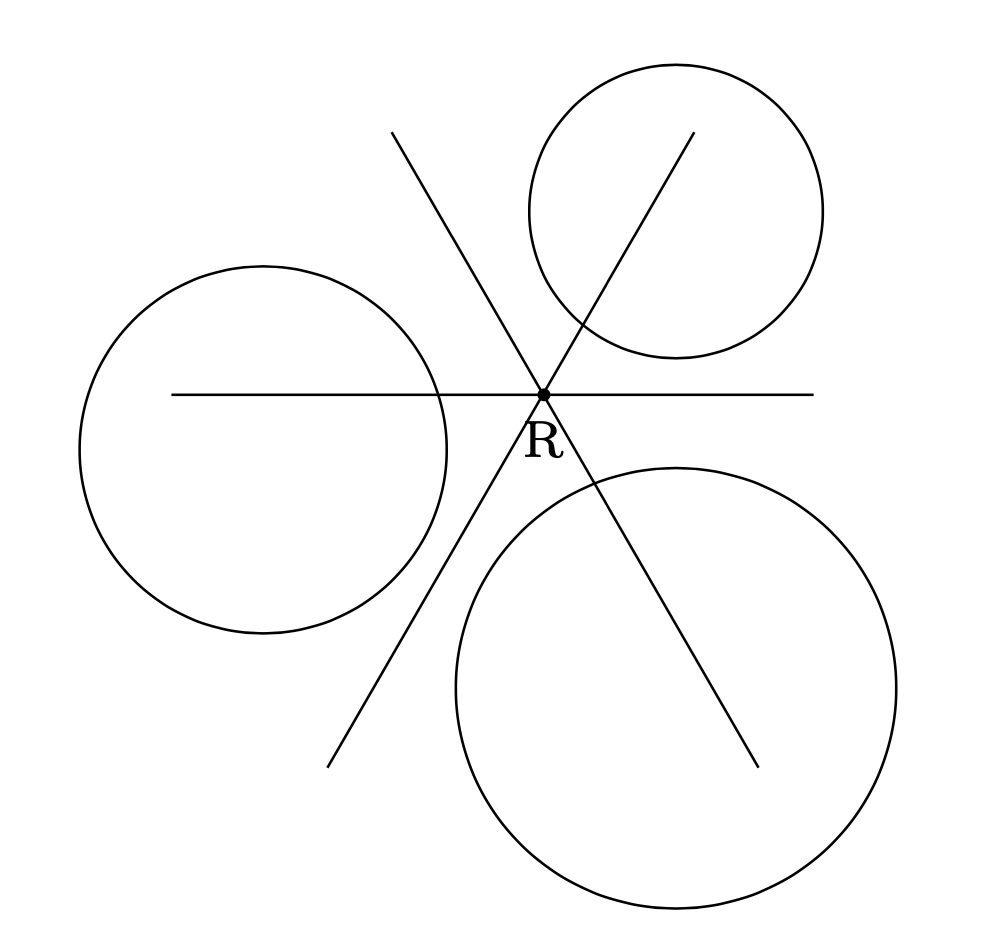根軸とは, 同心円でない2つの円に対する 方べきの値 が等しい点の集まりのことをいう.
以下,同心円でない2つの円
$$C_1:(x-a_1)^2+(y-b_1)^2=r_1^2$$
$$C_2:(x-a_2)^2+(y-b_2)^2=r_2^2$$
を考える.
まず,次の命題を証明する.
- 同心円でない2つの円\(C_1\),\(C_2\)の根軸は,直線である.
- 同心円でない2つの円\(C_1\),\(C_2\)の根軸は,中心を結ぶ直線に対して垂直である.
- 交わらない場合
- 接する場合
- 2点で交わる場合
そして,最後に次の根軸定理を証明する.
根軸定理
どの2つも同心円でない3つの円
\(C_1\),\(C_2\),\(C_3\)を考える.
\(C_1\)と\(C_2\),
\(C_2\)と\(C_3\),
\(C_3\)と\(C_1\)の根軸をそれぞれ
\(\ell_{12}\),\(\ell_{23}\),\(\ell_{31}\)とする.
この時,
\(\ell_{12}\),\(\ell_{23}\),\(\ell_{31}\)は平行であるか,
1点で交わる.
後者の場合,
その点を根心と言う.