- \(\sin(\alpha+\beta) =\sin\alpha\cos\beta+\cos\alpha\sin\beta\)
- \(\cos(\alpha+\beta) =\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
- \(\tan(\alpha+\beta) =\displaystyle\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)
- \(\sin(\alpha-\beta) =\sin\alpha\cos\beta-\cos\alpha\sin\beta\)
- \(\cos(\alpha-\beta) =\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
- \(\tan(\alpha-\beta) =\displaystyle\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\)
次に,上で証明した加法定理を用いて, 三角比の合成と呼ばれる次の計算が成り立つことを証明する.
三角関数を含む式
\(a\sin\theta+b\cos\theta\)は次のように変形できる.
$$a\sin\theta+b\cos\theta=r\sin(\theta+\alpha)$$
ただし,
\(r\),\(\alpha\)は
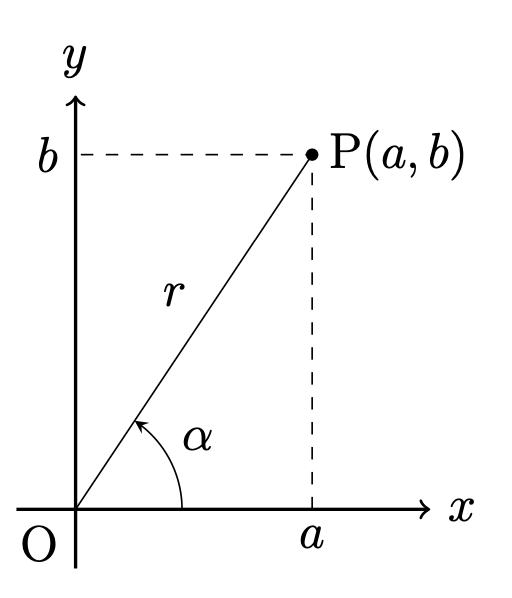
右図の通りとする.
すなわち, \(a,b\)に対して, 次が成り立つようなものである. $$r=\sqrt{a^2+b^2} ,\hspace{5pt}\cos\alpha=\frac{a}{r} ,\hspace{5pt}\sin\alpha=\frac{b}{r} $$
すなわち, \(a,b\)に対して, 次が成り立つようなものである. $$r=\sqrt{a^2+b^2} ,\hspace{5pt}\cos\alpha=\frac{a}{r} ,\hspace{5pt}\sin\alpha=\frac{b}{r} $$