まずは,正三角形では,五心のうち傍心を除く4つの点が一致することを証明する.
定理.
正三角形において,
外心,内心,重心,垂心は一致する.
五心は全て三角形に対して定義される3直線の交点として定義されるが,
正三角形においては,それらの直線が等しいことを言えばよい.
また傍心についての結果にも触れる.
定理.
正三角形\(\bigtriangleup{\rm{ABC}}\)において, 頂角\({\rm{A}}\)内の傍心は, その対辺\({\rm{BC}}\)に関して, 頂点\({\rm{A}}\)と対称な位置にある. 他の頂角内の傍心についても同様である.
正三角形\(\bigtriangleup{\rm{ABC}}\)において, 頂角\({\rm{A}}\)内の傍心は, その対辺\({\rm{BC}}\)に関して, 頂点\({\rm{A}}\)と対称な位置にある. 他の頂角内の傍心についても同様である.
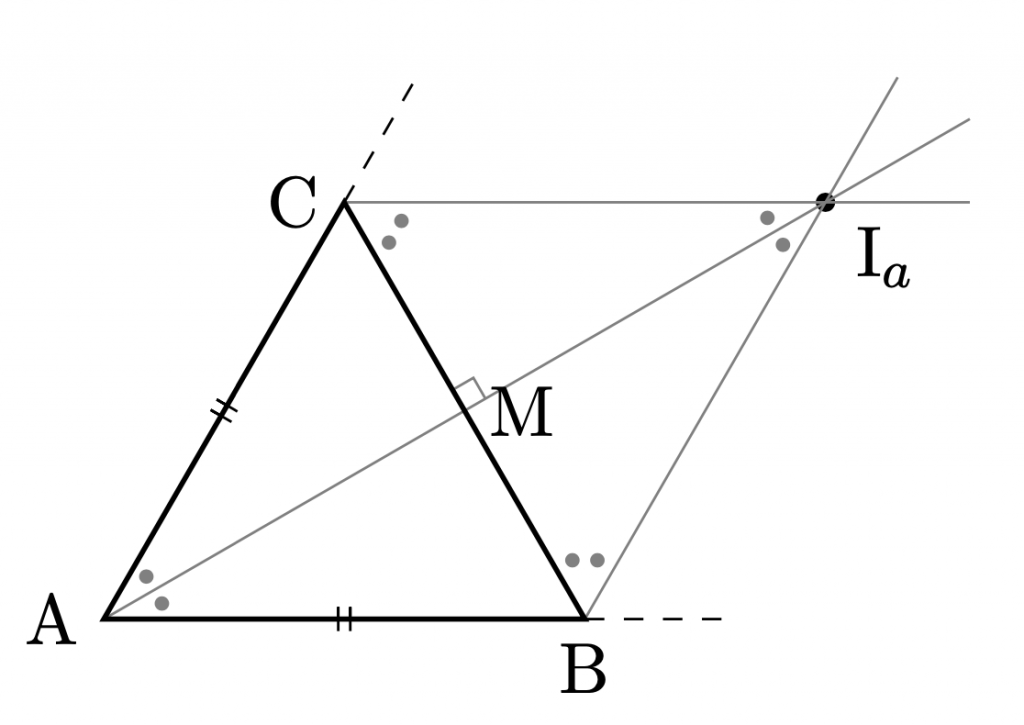
最後に, 最初の定理の逆を考察する. すなわち,外心,内心,重心,垂心が一致する三角形は, 正三角形であるかという問いを考える. これについては, 4点が一致している必要はなく, 2点が一致していれば十分であるというのが次の定理である.
定理.
ある三角形において,
外心,内心,重心,垂心のうち2点が一致するとき,
この三角形は正三角形である.
(すなわち,他の2点も一致する.)
証明は,2段階で行う.
まず補題として,次を示す.
補題. \(\bigtriangleup{\rm{ABC}}\)において, 頂点\({\rm{A}}\)を通る直線であって, 次の3つの性質のうち2つを満たすものが存在するとき, \(\bigtriangleup{\rm{ABC}}\)は, 辺\({\rm{BC}}\)を底辺とする二等辺三角形である.
- (性質1) 頂点\({\rm{A}}\)の内角を二等分する.
- (性質2) 辺\({\rm{BC}}\)と垂直である.
- (性質3) 辺\({\rm{BC}}\)を二等分する.
その次に, 外心,内心,重心,垂心を定義する直線が, それぞれ次のように上の補題の性質を備えていることから
- 辺\({\rm{BC}}\)の垂直二等分線は,補題の性質2,3を満たす. (頂点\({\rm{A}}\)を通るかはわからない.)
- 頂点\({\rm{A}}\)の内角の二等分線は,頂点\({\rm{A}}\)を通り,補題の性質1を満たす.
- 頂点\({\rm{A}}\)から対辺\({\rm{BC}}\)に引いた中線は,頂点\({\rm{A}}\)を通り,補題の性質3を満たす.
- 頂点\({\rm{A}}\)から対辺\({\rm{BC}}\)に下ろした垂線は,頂点\({\rm{A}}\)を通り,補題の性質2を満たす.
